/Konkursy/Olimpiada Matematyczna/60 (LX)

LX Olimpiada Matematyczna I stopień 2008/2009

I seria

Zadanie 1

Na niektórych polach szachownicy rozmiaru 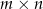m × n ustawiono wieże. Wiadomo, że dowolna wieża znajduje się w polu rażenia co najwyżej dwóch innych wież. Wyznaczyć, w zależności od 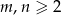m ,n ≥ 2 , największą liczbę wież na szachownicy, dla której taka sytuacja jest możliwa.

Zadanie 2

Dana jest liczba całkowita 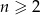n ≥ 2 . Niech 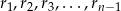r,r ,r ,...,r 1 2 3 n−1 będą odpowiednio resztami z dzielenia liczb

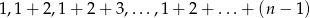
1,1+ 2,1+ 2+ 3,...,1+ 2+ ...+ (n − 1)

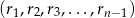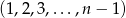przez . Znaleźć wszystkie takie wartości , że ciąg (r1,r2,r3,...,rn− 1) jest permutacją ciągu (1,2,3 ,...,n − 1) .

Zadanie 3

Okrąg wpisany w trójkąt 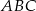ABC jest styczny do boków 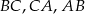BC ,CA ,AB odpowiednio w punktach 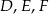D ,E ,F . Punkty 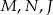M ,N ,J są odpo- wiednio środkami okręgów wpisanych w trójkąty 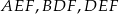AEF ,BDF ,DEF . Dowieść, że punkty 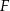i 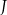są symetryczne względem prostej .

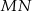Zadanie 4

Udowodnić, że dla dowolnych nieujemnych liczb rzeczywistych 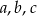a,b,c prawdziwa jest nierówność

√ ----- √ ----- √ ---- 4( a3b3 + b3c3 + c3a3) ≤ 4c3 + (a+ b)3.

Wersja PDF