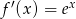/Studia/Analiza

Zadanie nr 1030940

Dodaj do ulubionych
Dodaj do rozwiązanych

Korzystając ze wzoru 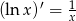′ 1 (ln x) = x oblicz pochodną funkcji x f(x) = e .

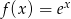Rozwiązanie

Sposób I

Różniczkujemy stronami równość

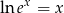
x ln e = x

korzystając z podanego wzoru na pochodną logarytmu i ze wzoru na pochodną funkcji złożonej.

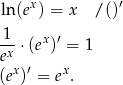
x ′ ln (e ) = x / () 1- x ′ ex ⋅(e ) = 1 (ex)′ = ex.

Sposób II

Korzystamy ze wzoru

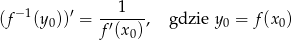
− 1 ′ --1---- (f (y 0)) = f′(x0), gdzie y 0 = f(x0)

na pochodną funkcji odwrotnej.

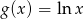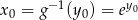Jeżeli oznaczmy g (x) = ln x to −1 y0 x0 = g (y0) = e i na mocy powyższego wzoru mamy

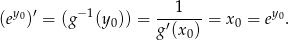
(ey0)′ = (g−1(y0)) = --1----= x0 = ey0. g′(x0)

Zamieniając literkę z 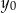y 0 na x otrzymujemy (ex)′ = ex .  
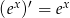Odpowiedź: f′(x) = ex

Wersja PDF