/Studia/Analiza

Zadanie nr 1050336

Dodaj do ulubionych
Dodaj do rozwiązanych

Napisz równanie stycznej do krzywej 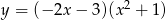2 y = (− 2x − 3)(x + 1) w punkcie x0 = − 3 .

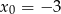Rozwiązanie

Będziemy korzystać z tego, że współczynnik kierunkowy stycznej do wykresu funkcji 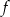f w punkcie 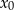x0 jest równy pochodnej 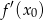f′(x0) w tym punkcie. Można też od razu skorzystać ze wzoru na styczną

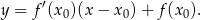
y = f′(x0)(x− x0)+ f(x0).

Liczymy pochodną

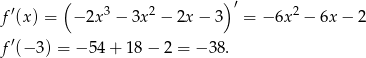
( ) f′(x) = − 2x3 − 3x2 − 2x − 3 ′ = −6x 2 − 6x− 2 f′(− 3) = − 54 + 18 − 2 = −3 8.

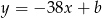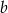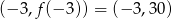Zatem styczna jest postaci y = − 38x + b . Współczynnik b wyliczamy z tego, że ma ona przechodzić przez punkt (− 3,f(− 3)) = (−3 ,30) .

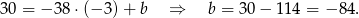
3 0 = − 38 ⋅(− 3)+ b ⇒ b = 30 − 114 = − 84.

 
Odpowiedź: y = − 3 8x− 84

Wersja PDF