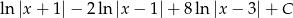/Studia/Analiza

Zadanie nr 1126778

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz całkę 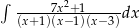∫ ----7x2+1------ (x+ 1)(x− 1)(x−3)dx .

Rozwiązanie

Mianownik ma trzy czynniki liniowe, każdy w pierwszej potędze, więc funkcja podcałkowa jest sumą trzech ułamków prostych pierwszego rodzaju:

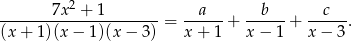
-------7x-2 +-1------- --a--- --b--- --c--- (x + 1)(x − 1)(x − 3 ) = x + 1 + x− 1 + x − 3 .

Mnożąc obie strony przez 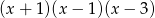(x+ 1)(x− 1)(x − 3) otrzymujemy

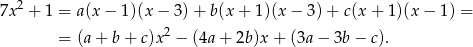
7x2 + 1 = a(x − 1)(x − 3) + b(x + 1 )(x− 3)+ c(x + 1)(x− 1) = 2 = (a + b+ c)x − (4a+ 2b)x + (3a − 3b − c).

Porównując współczynniki po obu stronach dostajemy układ równań

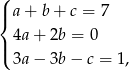
( | a+ b+ c = 7 { | 4a+ 2b = 0 ( 3a− 3b − c = 1,

Dodając pierwsze i trzecie równanie stronami mamy 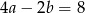4a − 2b = 8 . Dodając do tego równania drugie równanie mamy 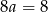8a = 8 , czyli 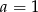a = 1 . Stąd (z drugiego równania) 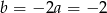b = − 2a = − 2 i (z pierwszego równania) 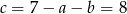c = 7− a− b = 8 . Stąd

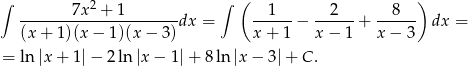
∫ 7x2 + 1 ∫ ( 1 2 8 ) ----------------------dx = ------− ------+ ------ dx = (x + 1)(x − 1)(x − 3) x+ 1 x − 1 x− 3 = ln|x + 1|− 2ln |x − 1 |+ 8 ln |x− 3|+ C .

 
Odpowiedź: ln |x+ 1|− 2 ln |x − 1|+ 8ln|x − 3| + C

Wersja PDF