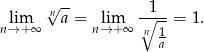/Studia/Analiza

Zadanie nr 1264186

Dodaj do ulubionych
Dodaj do rozwiązanych

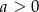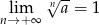Udowodnij, że jeżeli a > 0 to n√ -- nl→im+ ∞ a = 1 .

Rozwiązanie

Jeżeli 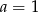a = 1 to ciąg jest stały i teza jest oczywista. Załóżmy więc, że a ⁄= 1 .

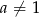Na początek rozważmy przypadek 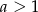a > 1 . Chcemy jakoś oszacować

√ -- na − 1.

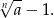
Sposób I

Standardowy sposób na tego typu szacowania to tak zwana nierówność Bernoulliego

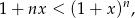
1+ nx < (1 + x )n,

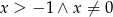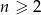prawdziwa dla x > − 1 ∧ x ⁄= 0 oraz n ≥ 2 . Dla dodatniego x (a tak będzie u nas) nierówność ta jest prostym wnioskiem ze wzoru dwumianowego Newtona, a w pełnej ogólności łatwo ją uzasadnić indukcyjnie.

Korzystając z tej nierówności dla 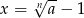√ -- x = na − 1 mamy

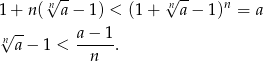
√n-- n√ -- n 1+ n( a − 1) < (1+ a− 1) = a √n-- a−-1-- a − 1 < n .

Ponieważ ciąg 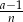a−1- n dąży do zera i 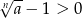-- √na − 1 > 0 , więc ciąg 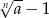-- n√ a− 1 też dąży do 0, czyli

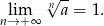
-- lim √na = 1 . n→ +∞

Sposób II

Możemy też sobie poradzić bez nierówności Bernoulliego. Ustalmy 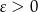𝜀 > 0 . Musimy pokazać, że dla prawie wszystkich n

√n-- a − 1 < 𝜀

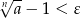
Spróbujemy rozwiązać tę nierówność.

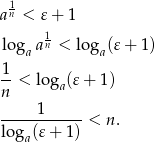
1 a n < 𝜀+ 1 -1 lo gaan < lo ga(𝜀+ 1) 1 -- < loga(𝜀 + 1) n -----1----- < n. loga (𝜀+ 1)

Widać, że dla prawie wszystkich n nierówność ta jest spełniona. Oczywiście po drodze mocno korzystaliśmy z założenia 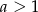a > 1 .

Pozostał przypadek 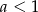a < 1 . Korzystając z podstawowych własności granic, łatwo się go sprowadza do poprzedniego.

lim √na--= lim ∘1-- = 1. n→ +∞ n→+ ∞ n 1 a
Wersja PDF