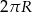/Studia/Analiza

Zadanie nr 1317095

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz długość okręgu o promieniu 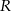R .

Rozwiązanie

Korzystamy ze wzoru

∫ b∘ ----------------- [x′(t)]2 + [y′(t)]2dt a

na długość krzywej o parametryzacji 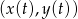(x(t),y(t)) , gdzie t ∈ [a,b] .

PIC

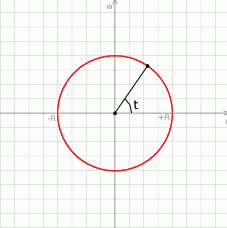
Okrąg o środku w 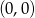(0,0) i promieniu 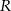R możemy sparametryzować następująco:

(x,y) = (R co st,R sin t), gdzie t ∈ [0,2π ].

Zatem długość okręgu jest równa

∫ ∘ ----------------- ∫ ∘ ------------------------ b ′ 2 ′ 2 2π 2 2 a [x (t)] + [y (t)]dt = 0 (−R sin t) + (R cost) dt = ∫ 2π ∘ -------------- ∫ 2π = R sin2 t+ co s2 tdt = R 1dt = 2πR . 0 0

 
Odpowiedź: 2πR

Wersja PDF