Zadanie nr 1337103
Oblicz granicę
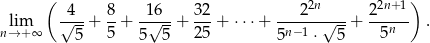
Rozwiązanie
Sposób I
Zauważmy, że wyrażenie w nawiasie jest sumą  początkowych wyrazów ciągu geometrycznego o pierwszym wyrazie
początkowych wyrazów ciągu geometrycznego o pierwszym wyrazie 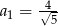 i ilorazie
i ilorazie 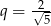 . W takim razie interesująca nas granica to suma wszystkich wyrazów ciągu
. W takim razie interesująca nas granica to suma wszystkich wyrazów ciągu 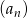 , czyli jest ona równa
, czyli jest ona równa
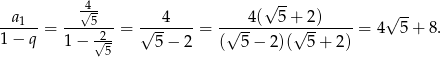
Sposób II
Zauważmy, że
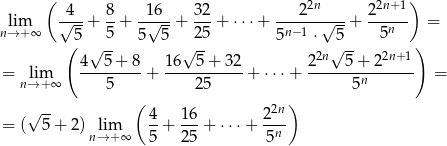
Widać teraz, że mamy do czynienia z sumą wszystkich wyrazów ciągu geometrycznego 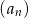 , w którym
, w którym 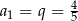 . Suma wszystkich wyrazów ciągu
. Suma wszystkich wyrazów ciągu 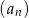 jest równa
jest równa
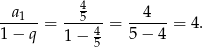
Interesująca nas granica jest więc równa
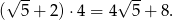
Odpowiedź: