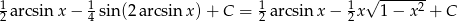Zadanie nr 1385056
Oblicz całkę 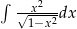 .
.
Rozwiązanie
Sposób I
Ponieważ 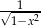 to dokładnie pochodna
to dokładnie pochodna 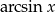 , możemy spróbować podstawić
, możemy spróbować podstawić 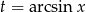 . Mamy wtedy
. Mamy wtedy 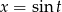 oraz
oraz
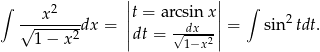
Teraz korzystamy ze wzoru 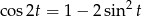 .
.
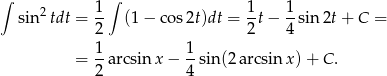
Sposób II
Podstawiamy 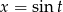 , gdzie
, gdzie ![t ∈ [− π2, π2]](https://img.zadania.info/zad/1385056/HzadR8x.gif) . Mamy wtedy
. Mamy wtedy
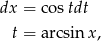
oraz
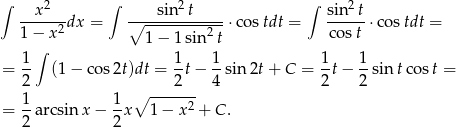
Odpowiedź: 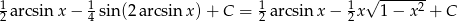
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 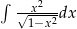 .
.
Sposób I
Ponieważ 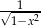 to dokładnie pochodna
to dokładnie pochodna 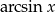 , możemy spróbować podstawić
, możemy spróbować podstawić 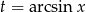 . Mamy wtedy
. Mamy wtedy 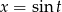 oraz
oraz
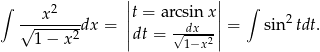
Teraz korzystamy ze wzoru 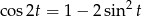 .
.
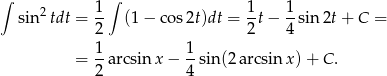
Sposób II
Podstawiamy 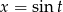 , gdzie
, gdzie ![t ∈ [− π2, π2]](https://img.zadania.info/zad/1385056/HzadR8x.gif) . Mamy wtedy
. Mamy wtedy
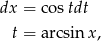
oraz
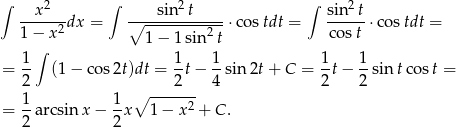
Odpowiedź: