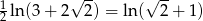Zadanie nr 1497384
Oblicz długość krzywej 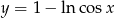 , gdzie
, gdzie 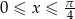 .
.
Rozwiązanie
Korzystamy ze wzoru
![∫ b ∘ ------------ 1+ [f′(x )]2dx a](https://img.zadania.info/zad/1497384/HzadR0x.gif)
na długość wykresu funkcji 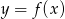 na przedziale
na przedziale ![[a,b]](https://img.zadania.info/zad/1497384/HzadR2x.gif) .
.
W naszej sytuacji mamy
![∘ -------------- ∫ b∘ ------------ ∫ π4 ( sinx ) 2 1 + [f′(x)]2dx = 1 + ----- dx = a 0 cosx ∫ π ∘ ------------2-- ∫ π ∫ π 4 cos2-x+--sin--x- 4--1-- 4-cosx- = 0 co s2 x dx = 0 co sxdx = 0 co s2xdx = | | ∫ √2 ∫ √2( ) || t = sin x || 2 --dt-- 1- 2 --1-- --1-- = |dt = cos xdx| = 0 1 − t2 = 2 0 1 − t + 1 + t dt = √- √ - 1 √-2 1 [ 1+ t]-22 1 1 + --2 = -[− ln |1− t|+ ln|1 + t|]02 = -- ln ----- = -ln ----√2- = 2 2 1− t 0 2 1 − -22 √ -- √ --2 √ -- √ -- = 1ln 2-+-√-2-= 1-ln (2-+---2)--= 1-ln 4-+-4--2-+-2-= 1-ln (3+ 2 2). 2 2 − 2 2 4− 2 2 2 2](https://img.zadania.info/zad/1497384/HzadR3x.gif)
Mogliśmy też końcowy rachunek przeprowadzić odrobinę inaczej:
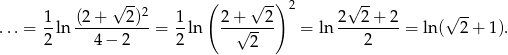
Odpowiedź: 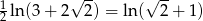
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz długość krzywej 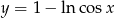 , gdzie
, gdzie 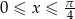 .
.
Korzystamy ze wzoru
![∫ b ∘ ------------ 1+ [f′(x )]2dx a](https://img.zadania.info/zad/1497384/HzadR0x.gif)
na długość wykresu funkcji 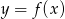 na przedziale
na przedziale ![[a,b]](https://img.zadania.info/zad/1497384/HzadR2x.gif) .
.
W naszej sytuacji mamy
![∘ -------------- ∫ b∘ ------------ ∫ π4 ( sinx ) 2 1 + [f′(x)]2dx = 1 + ----- dx = a 0 cosx ∫ π ∘ ------------2-- ∫ π ∫ π 4 cos2-x+--sin--x- 4--1-- 4-cosx- = 0 co s2 x dx = 0 co sxdx = 0 co s2xdx = | | ∫ √2 ∫ √2( ) || t = sin x || 2 --dt-- 1- 2 --1-- --1-- = |dt = cos xdx| = 0 1 − t2 = 2 0 1 − t + 1 + t dt = √- √ - 1 √-2 1 [ 1+ t]-22 1 1 + --2 = -[− ln |1− t|+ ln|1 + t|]02 = -- ln ----- = -ln ----√2- = 2 2 1− t 0 2 1 − -22 √ -- √ --2 √ -- √ -- = 1ln 2-+-√-2-= 1-ln (2-+---2)--= 1-ln 4-+-4--2-+-2-= 1-ln (3+ 2 2). 2 2 − 2 2 4− 2 2 2 2](https://img.zadania.info/zad/1497384/HzadR3x.gif)
Mogliśmy też końcowy rachunek przeprowadzić odrobinę inaczej:
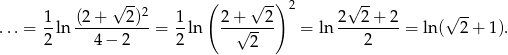
Odpowiedź: