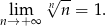Zadanie nr 1914802
Wykaż, że 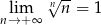 .
.
Rozwiązanie
Musimy jakoś oszacować z góry
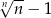
przez ciąg zbieżny do 0.
Ze wzoru dwumianowego Newtona, dla 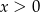 mamy nierówność
mamy nierówność
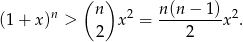
Zastosujmy tę nierówność do 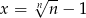 .
.
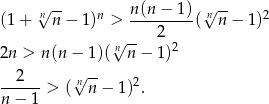
Ponieważ ciąg 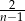 zbiega do 0, oraz prawa strona powyższej nierówności jest dodatnia, ciąg
zbiega do 0, oraz prawa strona powyższej nierówności jest dodatnia, ciąg 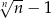 też zbiega do 0, czyli
też zbiega do 0, czyli