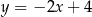Zadanie nr 2019206
Z punktu 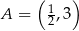 poprowadzono styczne do wykresu funkcji
poprowadzono styczne do wykresu funkcji 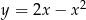 . Wyznacz równia tych stycznych.
. Wyznacz równia tych stycznych.
Rozwiązanie
Musimy sprawdzić w jakim punkcie styczna do wykresu 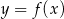 jest prostą przechodzącą przez punkt
jest prostą przechodzącą przez punkt 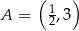 . Zacznijmy od wyznaczenia ogólnej postaci stycznej do danej funkcji w punkcie
. Zacznijmy od wyznaczenia ogólnej postaci stycznej do danej funkcji w punkcie 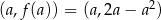 . Liczymy pochodną.
. Liczymy pochodną.
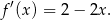
Styczna do paraboli w punkcie 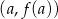 ma więc współczynnik kierunkowy równy
ma więc współczynnik kierunkowy równy 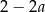 , czyli jest to prosta o równaniu
, czyli jest to prosta o równaniu
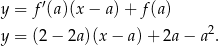
Sprawdzamy teraz kiedy styczna przechodzi przez dany punkt 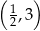 .
.
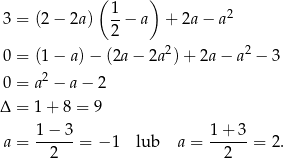
Styczne mają więc równania
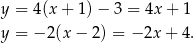
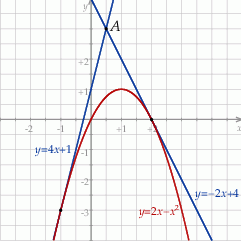
Odpowiedź: 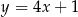 i
i