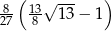Zadanie nr 2277304
Oblicz długość krzywej 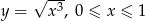 .
.
Rozwiązanie
Korzystamy ze wzoru
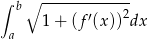
na długość wykresu funkcji 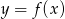 na przedziale
na przedziale ![[a,b]](https://img.zadania.info/zad/2277304/HzadR2x.gif) .
.
Szukana długość jest więc równa
![∘ -------------- ∘ ------------ ∫ 1 [( 3) ′] 2 ∫ 1 [3 1]2 1 + x2 dx = 1 + --x2 dx = 0 0 2 ∫ 1 ∘ ----9-- || 9 || = 1 + -xdx = ||t = 1+9 4x,|| = 0 4 dt = 4dx ∫ 13 √ - [ √ --] 134- ( √ --- ) = 4 4- tdt = 4⋅ 2- t3 = 8-- 1-3 13 − 1 . 1 9 9 3 1 27 8](https://img.zadania.info/zad/2277304/HzadR3x.gif)
Odpowiedź: 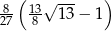
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz długość krzywej 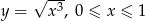 .
.
Korzystamy ze wzoru
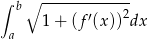
na długość wykresu funkcji 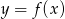 na przedziale
na przedziale ![[a,b]](https://img.zadania.info/zad/2277304/HzadR2x.gif) .
.
Szukana długość jest więc równa
![∘ -------------- ∘ ------------ ∫ 1 [( 3) ′] 2 ∫ 1 [3 1]2 1 + x2 dx = 1 + --x2 dx = 0 0 2 ∫ 1 ∘ ----9-- || 9 || = 1 + -xdx = ||t = 1+9 4x,|| = 0 4 dt = 4dx ∫ 13 √ - [ √ --] 134- ( √ --- ) = 4 4- tdt = 4⋅ 2- t3 = 8-- 1-3 13 − 1 . 1 9 9 3 1 27 8](https://img.zadania.info/zad/2277304/HzadR3x.gif)
Odpowiedź: