Poradnik stanowi kontynuację poradnika o funkcjach - radzimy tam zajrzeć w celu przypomnienia najważniejszych pojęć dotyczących funkcji. Składanie funkcji Bardzo ważną cechą funkcji jest to, że (czasami) można funkcje wykonywać jedna po drugiej.
Niech 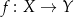 oraz
oraz 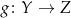 . Funkcję
. Funkcję 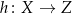 daną wzorem
daną wzorem
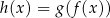
nazywamy złożeniem (superpozycją) funkcji 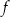 i
i 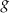 oraz oznaczamy
oraz oznaczamy 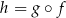 .
.
W pierwszej chwili można się zagubić w różnych literkach występujących w powyższej definicji, dlatego warto zapamiętać poniższy diagram:
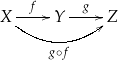
Jeżeli 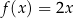 i
i 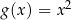 to
to
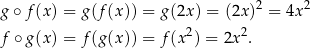
Jeżeli 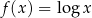 i
i 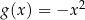 to
to
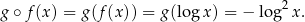
Złożenie 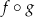 natomiast nie ma sensu, bo logarytmować możemy tylko liczby dodatnie.
natomiast nie ma sensu, bo logarytmować możemy tylko liczby dodatnie.
Funkcja odwrotna Jeżeli myślimy o funkcji 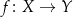 jak o zbiorze strzałek, które przyporządkowują elementom zbioru
jak o zbiorze strzałek, które przyporządkowują elementom zbioru 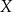 (dziedziny) elementy zbioru
(dziedziny) elementy zbioru 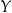 (przeciwdziedziny), to funkcja odwrotna
(przeciwdziedziny), to funkcja odwrotna 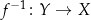 ma być przyporządkowaniem działającym dokładnie na odwrót, tzn. ma przyporządkowywać elementom zbioru
ma być przyporządkowaniem działającym dokładnie na odwrót, tzn. ma przyporządkowywać elementom zbioru 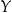 elementy zbioru
elementy zbioru 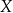 na odwrót niż robi to funkcja
na odwrót niż robi to funkcja 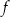 .
.
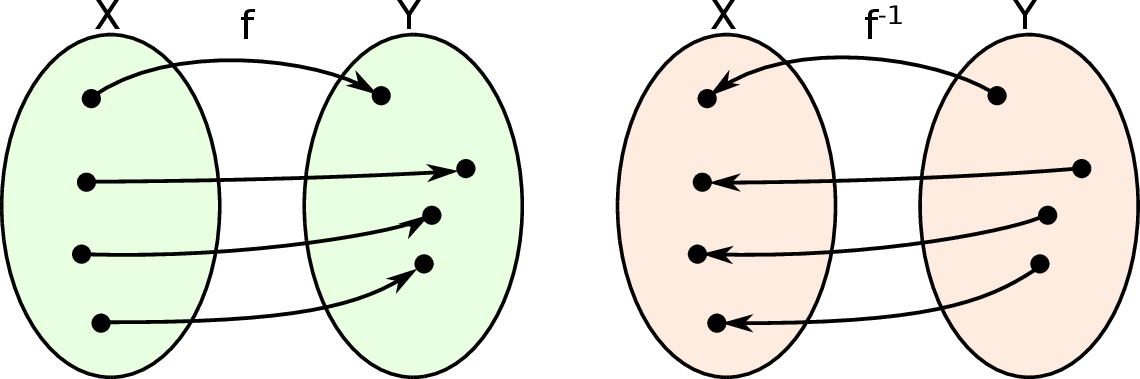
W języku powyższego obrazka, zamiana funkcji na funkcję odwrotną polega na zmianie zwrotów wszystkich strzałek.
Bardziej precyzyjną definicją funkcji odwrotnej 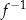 jest warunek:
jest warunek:
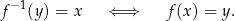
Nie każda funkcja 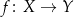 posiada funkcję odwrotną.
posiada funkcję odwrotną.
Funkcja 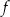 na lewym diagramie nie posiada funkcji odwrotnej, bo są różne strzałki prowadzące do tego samego elementu zbioru
na lewym diagramie nie posiada funkcji odwrotnej, bo są różne strzałki prowadzące do tego samego elementu zbioru 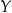 (funkcja
(funkcja 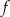 nie jest różnowartościowa). W przypadku funkcji
nie jest różnowartościowa). W przypadku funkcji 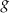 na prawym diagramie problemem jest to, że nie każdy element zbioru
na prawym diagramie problemem jest to, że nie każdy element zbioru 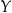 jest końcem pewnej strzałki (funkcja
jest końcem pewnej strzałki (funkcja 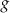 nie jest „na” zbiór
nie jest „na” zbiór 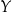 ).
).
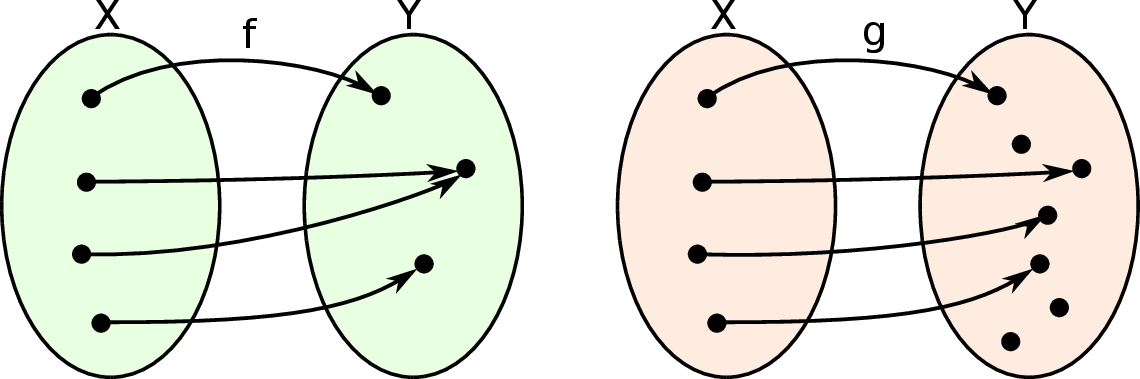
W obu przypadkach zmiana zwrotów strzałek prowadzi do przyporządkowania, które nie jest funkcją.
Podsumowując,
funkcja 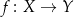 posiada funkcję odwrotną wtedy i tylko wtedy, gdy
posiada funkcję odwrotną wtedy i tylko wtedy, gdy 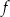 jest wzajemnie jednoznaczna, tzn. gdy jest różnowartościowa i „na”.
jest wzajemnie jednoznaczna, tzn. gdy jest różnowartościowa i „na”.
Wyznaczmy funkcję odwrotną do funkcji 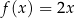 .
.
Funkcja 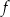 wysyła liczbę
wysyła liczbę  na liczbę
na liczbę 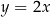 . Funkcja odwrotna wysyła w takim razie liczbę
. Funkcja odwrotna wysyła w takim razie liczbę 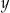 na liczbę
na liczbę 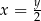 . Jest to więc funkcja:
. Jest to więc funkcja: 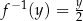 .
.
Na ogół jednak argument funkcji oznaczamy literką  (mówiąc inaczej: rysując wykres argumenty zaznaczamy na osi
(mówiąc inaczej: rysując wykres argumenty zaznaczamy na osi 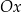 , a nie
, a nie 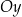 ), więc ostatni wzór zapisujemy w postaci
), więc ostatni wzór zapisujemy w postaci 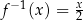 .
.
Jeżeli chwilę się zastanowimy, to powyższy rachunek ma sens: funkcja 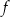 zmienia liczby mnożąc je przez 2, aby odwrócić skutki tej operacji musimy liczby dzielić przez 2.
zmienia liczby mnożąc je przez 2, aby odwrócić skutki tej operacji musimy liczby dzielić przez 2.
Funkcja 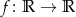 dana wzorem
dana wzorem 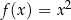 nie posiada funkcji odwrotnej, bo nie jest ani różnowartościowa, ani „na”. Spróbujmy poprawić funkcję
nie posiada funkcji odwrotnej, bo nie jest ani różnowartościowa, ani „na”. Spróbujmy poprawić funkcję 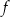 tak, aby była wzajemnie jednoznaczna. Zmieniając przeciwdziedzinę na przedział
tak, aby była wzajemnie jednoznaczna. Zmieniając przeciwdziedzinę na przedział 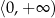 sprawiamy, że funkcja jest „na”. Aby rozwiązać problem różnowartościowości zmieniamy dziedzinę na przedział
sprawiamy, że funkcja jest „na”. Aby rozwiązać problem różnowartościowości zmieniamy dziedzinę na przedział 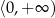 .
.
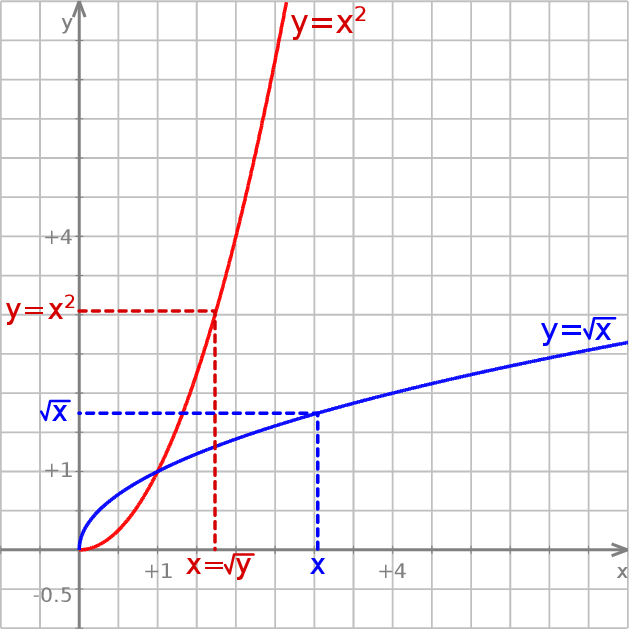
Tak poprawiona funkcja 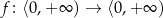 posiada funkcję odwrotną i jest nią funkcja:
posiada funkcję odwrotną i jest nią funkcja: 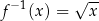 .
.
Funkcja logarytmiczna 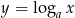 , gdzie
, gdzie 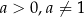 jest zdefiniowana jako funkcja odwrotna do funkcji wykładniczej
jest zdefiniowana jako funkcja odwrotna do funkcji wykładniczej 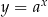 .
.
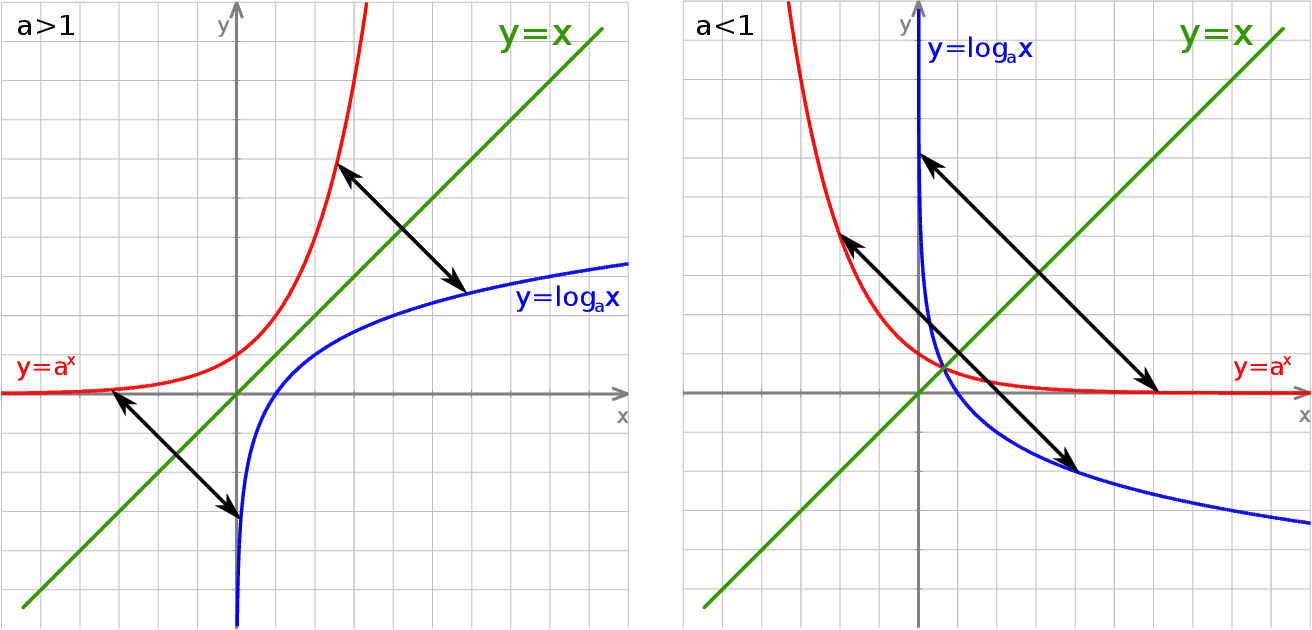
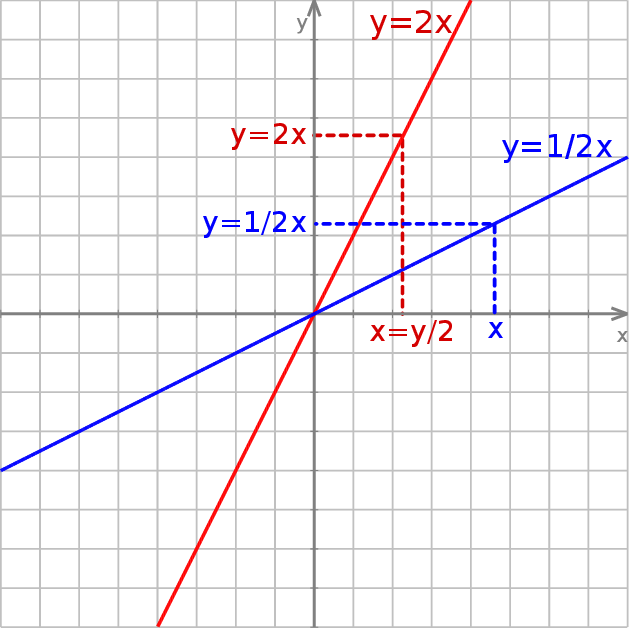
Przyglądając się definicji funkcji odwrotnej nie jest trudno zauważyć, że wykresy funkcji 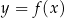 i
i 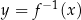 są symetryczne względem prostej
są symetryczne względem prostej 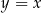 . Symetria ta pozwala łatwo naszkicować np. wykres funkcji
. Symetria ta pozwala łatwo naszkicować np. wykres funkcji 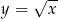 jako odbicie prawej gałęzi paraboli
jako odbicie prawej gałęzi paraboli 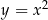 . Symetrię tę dobrze też widać na przykładzie funkcji
. Symetrię tę dobrze też widać na przykładzie funkcji 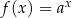 i
i 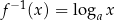 .
.