Zadanie nr 2814668
Oblicz całkę 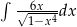 .
.
Rozwiązanie
Sposób I
Podstawiamy 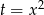 aby sprowadzić wyrażenie podcałkowe do pochodnej
aby sprowadzić wyrażenie podcałkowe do pochodnej 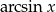 .
.
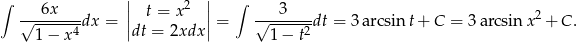
Sposób II
Ponieważ
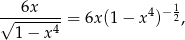
więc mamy do czynienia z różniczką dwumienną postaci
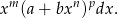
W naszej sytuacji mamy
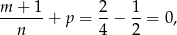
więc możemy podstawić 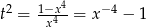 (jest to ogólna metoda całkowania różniczek dwumiennych). Mamy wtedy
(jest to ogólna metoda całkowania różniczek dwumiennych). Mamy wtedy
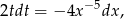
oraz
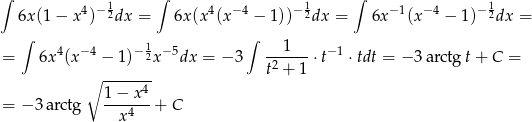
Odpowiedź: