/Studia/Analiza

Funkcje trygonometryczne

Są cztery funkcje trygonometryczne: 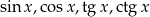sin x,cos x,tgx ,ctg x . Różnią się one zasadniczo od innych poznawanych w szkole funkcji z dwóch powodów: są okresowe oraz jest niezwykle dużo ciekawych zależności między nimi, czyli tzw. tożsamości trygonometrycznych. Ta druga własność sprawia, że zadania z trygonometrii sprawiają kłopoty – trzeba trochę wprawy, żeby wiedzieć jaki wzór pasuje do jakiego zadania. Sinus i cosinus Funkcje sinus i cosinus mają podobne wykresy, ale są przesunięte względem siebie o π- 2 .

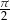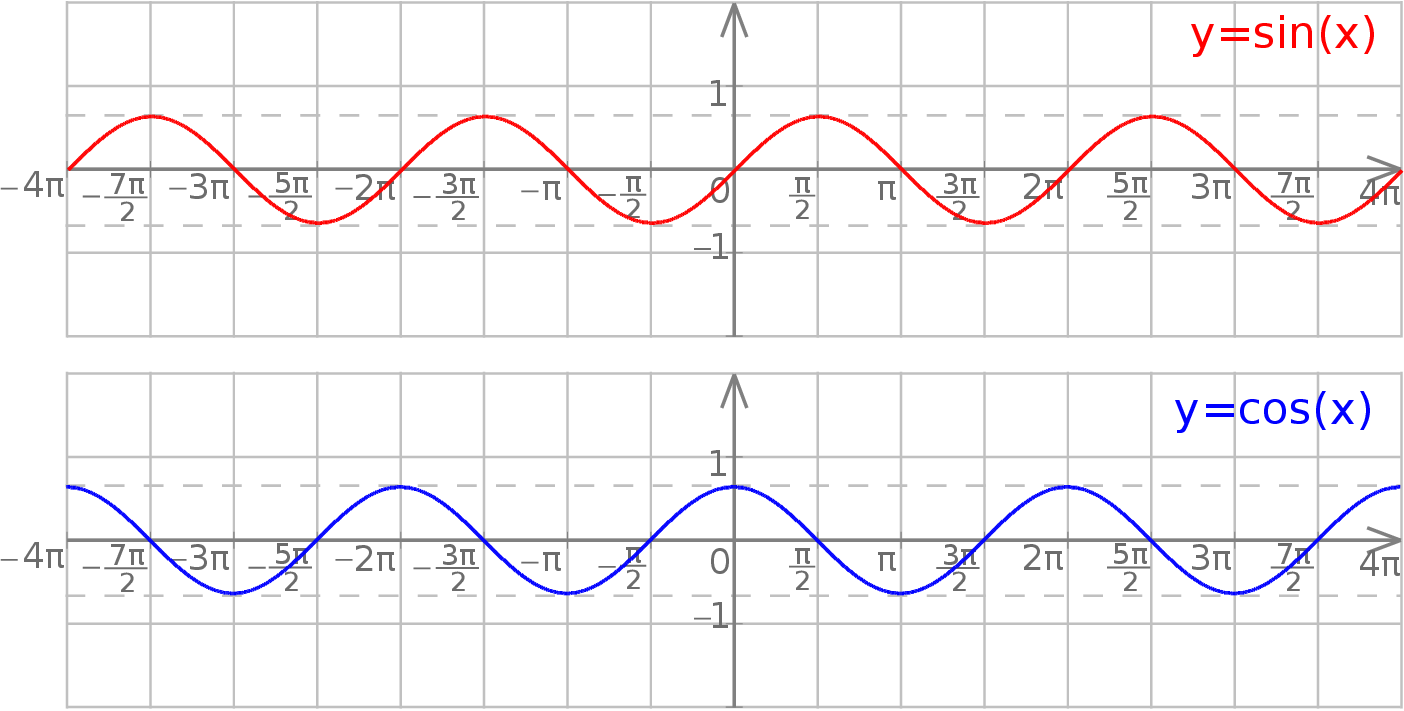
ZINFO-FIGURE

Obie funkcje są okresowe, co przejawia się tym, że ich wykresy powtarzają się – np. jeżeli weźmiemy kawałek wykresu sinusa na przedziale 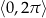⟨0,2π ⟩ , to cały wykres otrzymamy przesuwając ten kawałek o wielokrotności 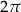2π w lewo i w prawo. Mówiąc jeszcze inaczej, wykresy tych funkcji nie zmieniają się przy przesuwaniu o wielokrotność 2π .

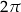W języku wzorków zapisuje się to w postaci

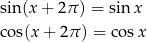
sin(x + 2π ) = sinx cos(x + 2 π) = co sx

Liczbę 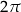2π nazywa się okresem podstawowym tych funkcji. Z tego, że liczba 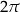2π jest okresem łatwo wynika, że dowolna jej wielokrotność też jest okresem, tzn.

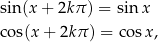
sin(x + 2k π) = sin x co s(x + 2kπ) = cosx,

gdzie 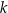k jest dowolną liczbą całkowitą.

Przymiotnik ’podstawowy’ przy okresie oznacza, że jest to najmniejszy okres, np. liczba 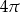4π też jest okresem tych funkcji (czyli 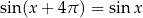sin(x + 4π ) = sinx ), ale nie jest okresem podstawowym.

Obliczmy 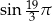sin 139π . Liczymy

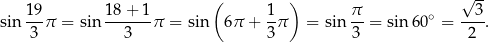
( ) √ -- 19 18 + 1 1 π ∘ 3 sin --π = sin ------π = sin 6π + -π = sin --= sin 60 = ---. 3 3 3 3 2

Tangens i cotangens Funkcje te są zdefiniowane zależności od funkcji sinus i cosinus:

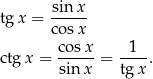
sin x tg x = cosx- ctg x = cosx-= -1--. sin x tg x

Z tych definicji powinno być jasne, że dziedziną funkcji 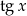tg x jest zbiór liczb, dla których 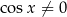cos x ⁄= 0 (czyli 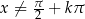x ⁄= π-+ kπ 2 ), a dziedziną funkcji 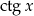ctg x zbiór liczb, dla których 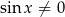sinx ⁄= 0 (czyli x ⁄= kπ ).

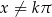Wykresy tych funkcji są podobne, ale funkcja tangens jest przedziałami rosnąca, a funkcja cotangens malejąca.

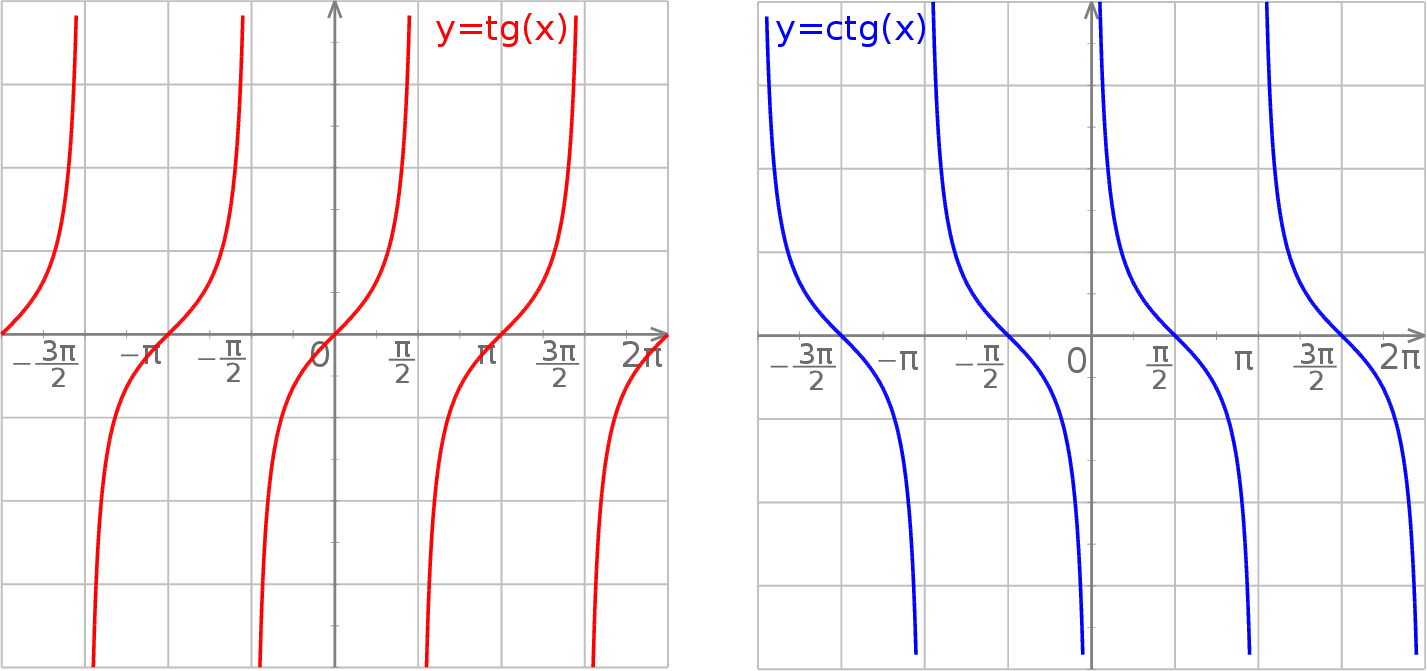
ZINFO-FIGURE

Rozerwania wykresów odpowiadają dokładnie miejscom zerowym mianowników. Obie funkcje mają okres podstawowy 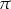π , czyli dwa razy mniejszy niż funkcje sinus i cosinus.

Obliczmy 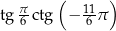π- ( 11 ) tg 6 ctg − 6 π . Liczymy

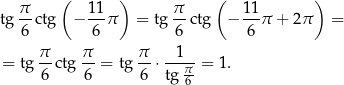
( ) ( ) π- 11- π- 11- tg 6 ctg − 6 π = tg 6 ctg − 6 π + 2π = = tg π-ctg π-= tg π ⋅--1--= 1. 6 6 6 tg π6-

Parzystość i nieparzystość Funkcja cosinus jest funkcją parzystą, tzn.

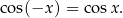
co s(−x ) = cos x.

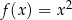Własność ta oznacza, że wykres jest symetryczny względem osi Oy . Można sobie myśleć, że jest podobnie jak dla f (x) = x2 , nie jest ważne, czy liczymy wartość funkcji w 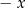− x czy w x (stąd ta symetria wykresu).

Funkcja sinus jest funkcją nieparzystą, tzn.

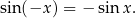
sin (−x ) = − sin x.

Własność ta oznacza, że wykres jest symetryczny względem początku (0,0) układu współrzędnych. Tu sytuacja jest podobna jak na przykład z f(x) = x 3 :

3 3 (− 2) = − 2 .

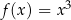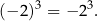
Obliczmy 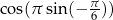π- cos(π sin(− 6 )) . Liczymy

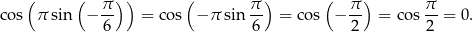
( ( π-) ) ( π-) ( π-) π- co s π sin − 6 = co s − π sin 6 = co s − 2 = cos 2 = 0.

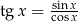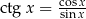Korzystając z powyższych własności oraz z równości tg x = scoinsxx- i ctgx = csoinsxx , łatwo wyliczyć, że funkcje tangens i cotangens są nieparzyste.

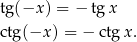
tg (−x ) = − tg x ctg (−x ) = − ctg x.

W przypadku funkcji parzystych/nieparzystych wygodnie jest myśleć, że ich wartości dla liczb ujemnych są jednoznacznie wyznaczone przez wartości dla liczb dodatnich. Punkty szczególne wykresów Rozwiązując różne zadania z funkcjami trygonometrycznymi często będziemy musieli ustalić jakie są ich miejsca zerowe lub kiedy sinus/cosinus jest równy ± 1 . Na wykresie punkty te odpowiadają punktom przecięcia z osią 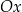Ox oraz górkom i dołkom sinusa/cosinusa.

sinx = 0 ⇐ ⇒ x = kπ cos x = 0 ⇐ ⇒ x = π-+ kπ 2 sinx = 1 ⇐ ⇒ x = π-+ 2kπ 2 cos x = 1 ⇐ ⇒ x = 2kπ sinx = − 1 ⇐ ⇒ x = − π-+ 2k π 2 cos x = − 1 ⇐ ⇒ x = π + 2kπ .

We wszystkich wzorach k ∈ C .

Miejsca zerowe tangensa i cotangensa są takie same jak odpowiednio sinusa i cosinusa:

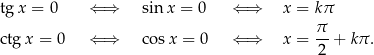
tg x = 0 ⇐ ⇒ sinx = 0 ⇐ ⇒ x = kπ π- ctg x = 0 ⇐ ⇒ cos x = 0 ⇐ ⇒ x = 2 + kπ.

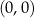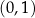Jedyny sposób, żeby się w tym nie pogubić, to nauczyć się szybko szkicować wykresy tych funkcji. W przypadku sinusa i cosinusa należy zapamiętać, że wykresem jest sinusoida przechodząca przez (0,0) i (0,1) odpowiednio. W przypadku tangensa i cotangensa wystarczy zapamiętać po jednej gałęzi wykresu i pamiętać, że całe wykresy otrzymujemy przesuwając je w lewo i w prawo.

Rozwiążmy równanie 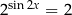2 sin2x = 2 . Liczymy

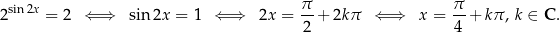
2sin2x = 2 ⇐ ⇒ sin 2x = 1 ⇐ ⇒ 2x = π-+ 2kπ ⇐ ⇒ x = π-+ kπ, k ∈ C. 2 4

Tips & Tricks

1Po co definiuje się funkcje trygonometryczne i dlaczego są one ważne?
Powody są geometryczne: funkcje trygonometryczne są łącznikiem między długościami odcinków, a miarami kątów. Na ogół, w zadaniach geometrycznych, nie da się wyliczyć dokładnej wartości szukanego kąta, jednak twierdzenia sinusów, cosinusów pozwalają wyliczyć (dokładnie!) ich funkcje trygonometryczne.

Nie jesteśmy w stanie wyliczyć miar kątów w trójkącie o bokach 5,6,7. Możemy natomiast (z twierdzenia cosinusów) wyliczyć cosinusy tych kątów.

2 Ze względu na okresowość, odpowiedzi do zadań z trygonometrii często są postaci 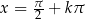x = π-+ kπ 2 . Domyślnie w takim zapisie, liczba 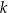k jest dowolną liczbą całkowitą.

Rozwiążmy równanie 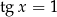tg x = 1 .
Wiemy, że 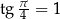tg π4 = 1 . Patrząc na wykres widać, że wszystkie rozwiązania to 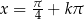x = π-+ kπ 4 , gdzie k ∈ C .

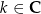3Trudno nie zauważyć, że wszędzie piszemy argumenty funkcji trygonometrycznych w radianach i jest ku temu powód. Jeżeli mówimy o funkcjach trygonometrycznych to chcemy, aby i argumenty i wartości to były liczbami, żeby np. miała sens funkcja 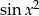sin x2 . Stopnie nie mają tej własności. Po więcej informacji na ten temat odsyłam do poradnika o mierze łukowej.

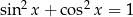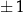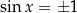4Z jedynki trygonometrycznej sin 2x + cos2 x = 1 łatwo wynika, że tam gdzie sinus się zeruje, cosinus jest równy ± 1 i odwrotnie. Ta własność bywa użyteczna przy rysowaniu tych funkcji lub przy sprawdzaniu czy dobrze pamiętamy, gdzie są punkty szczególne ich wykresów. Bywa też użyteczna przy równaniach typu sin x = ± 1 .

Rozwiążmy równanie 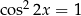2 co s 2x = 1

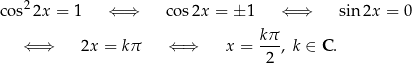
cos22x = 1 ⇐ ⇒ cos2x = ± 1 ⇐ ⇒ sin 2x = 0 ⇐ ⇒ 2x = kπ ⇐ ⇒ x = kπ, k ∈ C . 2

5 Niezwykle istotne jest pamiętanie, że zbiór wartości funkcji sinus i cosinus to przedział 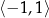⟨− 1,1⟩ . Takiej własności nie mają funkcje tangens i cotangens – one mogą przyjmować dowolne wartości.

Wyznaczmy zbiór wartości funkcji 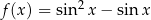2 f(x) = sin x− sin x .
Podstawiając 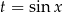t = sinx mamy parabolę 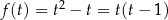2 f(t) = t − t = t(t − 1) obciętą do przedziału 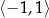⟨− 1,1⟩ (bo takie są wartości 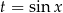t = sin x ). Aby ustalić jakie wartości przyjmuje ona w tym przedziale liczymy wartości w wierzchołku i w końcach przedziału

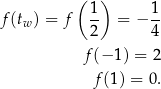
( 1 ) 1 f(tw) = f -- = − -- 2 4 f (− 1) = 2 f(1) = 0.

Zatem zbiór wartości to przedział 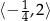1 ⟨− 4,2⟩ .

6Szczerze radzę nauczyć się podstawowych wartości funkcji trygonometrycznych na pamięć. Oczywiście można je sprawdzać w tablicach, ale trzeba pamiętać, że jednym z elementów każdego egzaminu jest walka z czasem. Na wertowanie tablic tracimy cenny czas, poza tym o wiele trudniej jest się pomylić, gdy wiemy, ile wynosi 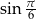π sin 6- , niż gdy tego nie wiemy, a przepisujemy z tabelki.

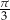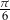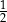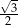Są różne sposoby pamiętania tych wartości. Na pewno trzeba zapamiętać, że sinus/cosinus kątów π3- i π6- to liczby 12 i √ - -23 . Która liczba, do którego kąta, i do której funkcji? Najlepiej jest zapamiętać, że dla kątów ostrych sinus jest rosnący, a cosinus malejący, więc musi być:

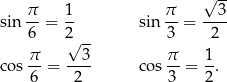
π 1 π √ 3- sin -- = -- sin -- = ---- 6 2√ -- 3 2 π 3 π 1 c os-6 = -2-- cos-3 = 2.

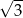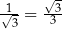Podobnie jest z tangensem i cotangensem tych kątów. Są to liczby √ -- 3 i 1 √ 3 √-3 = -3- . Która kiedy? – jak poprzednio: tangens jest rosnący, cotangens malejący. Zatem

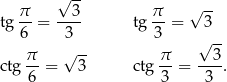
√ -- π 3 π √ -- tg -- = ---- tg --= 3 6 3 3 √ -- π- √ -- π- --3- ctg 6 = 3 ctg 3 = 3 .

Do tego jeszcze, dość łatwe do zapamiętania

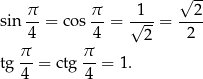
√ -- π- π- -1-- --2- sin 4 = cos 4 = √ 2 = 2 π π tg --= ctg-- = 1. 4 4

Akurat te równości łatwo sobie odtworzyć pamiętając o tym, że są to funkcje trygonometryczne w połówce kwadratu.

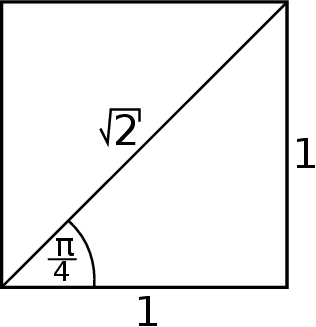
ZINFO-FIGURE

7Ciekawostka:

x ∘ 0 ∘ 3 0 ∘ 45 ∘ 60 ∘ 90
sinx √-0 2 √1- 2 √2- 2 √3- 2 √-4 2

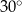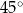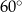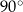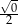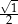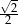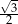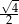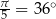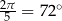8Okazuje się, że można również dokładnie wyliczyć funkcje trygonometryczne kątów π-= 3 6∘ 5 i 2π-= 7 2∘ 5 . Są one równe

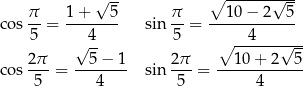
√ -- ∘ -------√--- cos π- = 1-+---5- sin π-= --10-−-2---5 5 4 5 ∘ --4------- 2π √ 5− 1 2π 1 0+ 2√ 5- cos --- = -------- sin ---= ------------ 5 4 5 4

Jeżeli ktoś jest ciekawy jak to się robi to niech zajrzy na https://www.zadania.info/3024938.

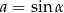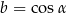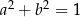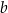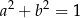9Wiemy, że jeżeli a = sin α i b = cosα to 2 2 a + b = 1 (jedynka trygonometryczna). Okazuje się, że jest też na odwrót: dane liczby a i b są sinusem i cosinusem pewnego kąta wtedy i tylko wtedy, gdy a2 + b2 = 1 .

Dla jakich wartości 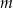m układ równań 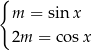{ m = sin x 2m = cos x ma rozwiązanie?
Zgodnie z tym, co powiedzieliśmy, układ będzie miał rozwiązanie jeżeli

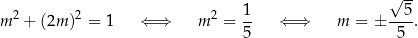
-- 1 √ 5 m 2 + (2m )2 = 1 ⇐ ⇒ m2 = -- ⇐ ⇒ m = ± ---. 5 5

10Zastanówmy się jak na komputerze narysować okrąg 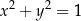2 2 x + y = 1 ? Nie jest to wykres funkcji, więc robi się to używając tzw. postaci parametrycznej:

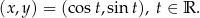
(x,y) = (cost,sint), t ∈ R .

Z jedynki trygonometrycznej jest jasne, że punkty tej postaci leżą na okręgu jednostkowym i gdy 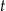t zmienia się w przedziale 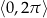⟨0,2π ⟩ to obiegają one cały okrąg.

ZINFO-FIGURE

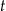Gdy t rośnie/maleje poza tym przedziałem to zaczynamy ponownie obiegać okrąg (z okresowości sinusa/cosinusa). Geometrycznie 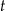t jest miarą kąta (w radianach) pomiędzy odcinkiem łączącym punkt 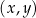(x ,y) z początkiem układu 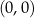(0,0) a osią 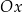Ox . Dla wielu osób to jest najprostszy sposób na zapamiętanie jakie są znaki sinusa i cosinusa w poszczególnych ćwiartkach – wystarczy pamiętać, że pierwsza współrzędna punktu 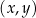(x,y) na okręgu to cosinus kąta, a druga to sinus. 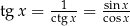Znaki tangensa i cotangensa łatwo ustalić pamiętając o definicji tgx = -1-- = sinx ctg x cosx .

Niech 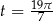t = 19π7 .
Koniec ramienia po obrocie o taki kąt będzie w II ćwiartce (bo 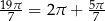19π = 2π + 5π-- 7 7 ). Zatem pierwsza współrzędna końca ramienia jest ujemna, a druga dodatnia. Mamy więc

co s(t) < 0 sin(t) > 0 tg(t) < 0 ctg(t) < 0.

11Powiedzieliśmy jak sparametryzować okrąg jednostkowy 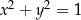2 2 x + y = 1 , a jak sparametryzować dowolny okrąg 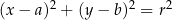2 2 2 (x − a) + (y − b) = r ? Podobnie:

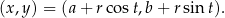
(x ,y) = (a+ rcos t,b+ r sin t).

Łatwo sprawdzić, że punkty tej postaci rzeczywiście są na tym okręgu.

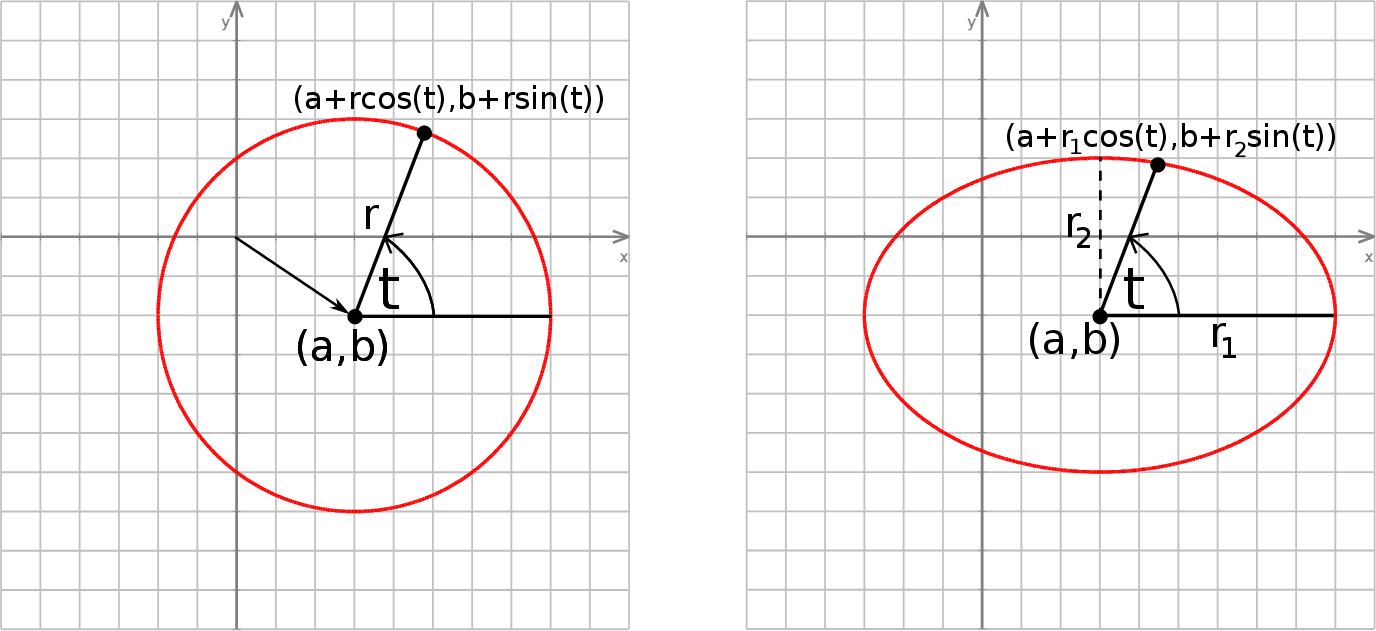
ZINFO-FIGURE

Jeżeli trochę to zmodyfikujemy

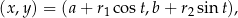
(x ,y) = (a + r1cos t,b+ r2 sin t),

to dostaniemy parametryzację elipsy (spłaszczonego okręgu) 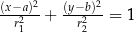(x−a)2 (y−b)2 --r2-- + --r2--= 1 1 2 .

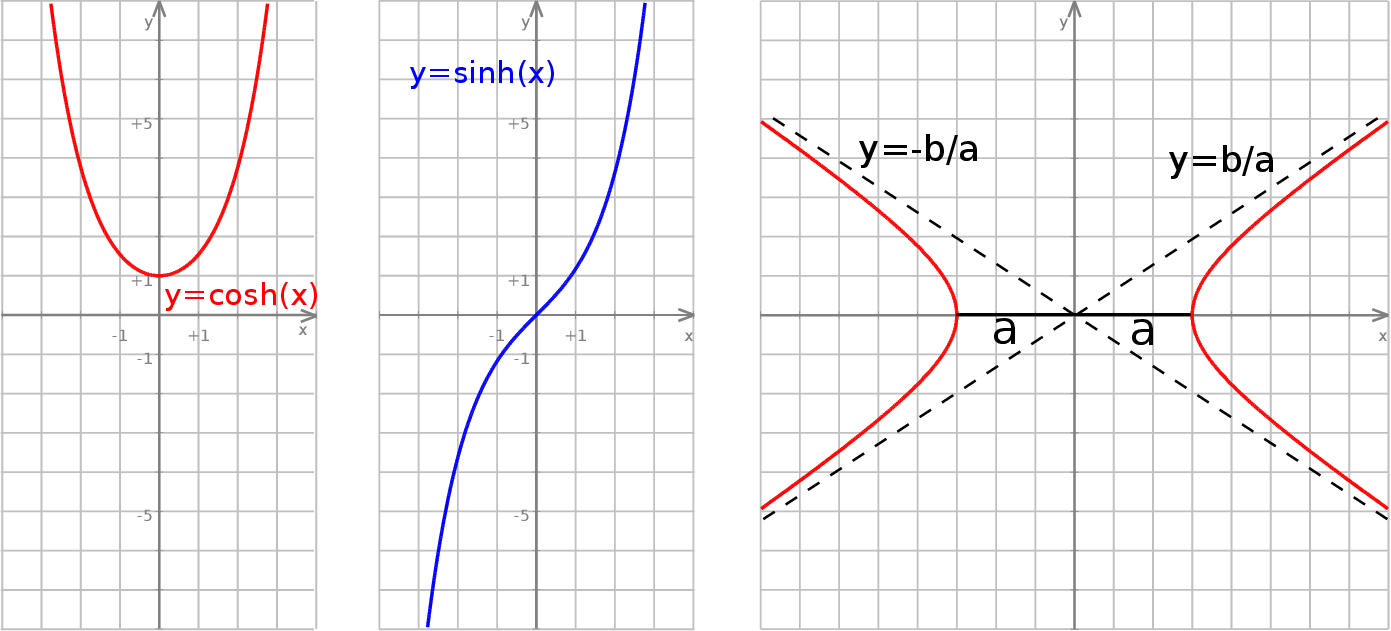
12Tak zupełnie poza szkolną matematyką, to są jeszcze funkcje

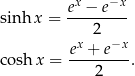
ex − e−x sin h x = --------- x 2 −x e--+-e--- cosh x = 2 .

Pomimo, że zdefiniowane dość dziwacznie mają one sporo własności podobnych do zwykłych funkcji trygonometrycznych (chociaż nie są okresowe!), np. spełniają równości

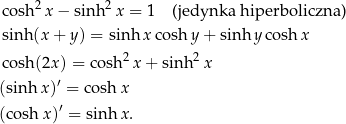
2 2 co sh x − sinh x = 1 (jedynka hiperboliczna ) sinh (x+ y) = sinh xco shy + sinh y cosh x co sh(2x) = cosh2x + sinh 2x ′ (sinh x) = cosh x (cosh x)′ = sinh x.

Skąd ich nazwa? – parametryzują one hiperbolę 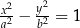2 x22 − y2-= 1 a b :

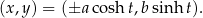
(x,y) = (±a cosh t,bsinh t).

Wybór znaku na pierwszej współrzędnej odpowiada wyborowi gałęzi hiperboli. Podobieństwo tych funkcji do funkcji trygonometrycznych jest dość głębokie, ale żeby o tym mówić, musielibyśmy wkroczyć w świat liczb zespolonych, a to już temat na inną opowieść.

ZINFO-FIGURE

13Tak naprawdę to są jeszcze różne inne funkcje trygonometryczne, o których się nie uczy w szkole, np. secans i cosecans:

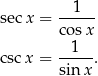
1 sec x = ----- cosx csc x = --1--. sin x

Można sobie wyobrazić, że gdy ich używamy to jest jeszcze więcej różnych rzeczy do zapamiętania, ale gdy ktoś przez to przebrnie, to potrafią one bardzo upraszczać zapis niektórych rachunków (gdy są sinusy/cosinusy w mianowniku).

W szkole jest tendencja dokładnie odwrotna, wszystko wskazuje na to, że niedługo zniknie ze szkoły funkcja cotangens.

14W jaki sposób kalkulator liczy wartości funkcji trygonometrycznych? Rysuje małe trójkąciki, mierzy boki i dzieli? Hm, raczej nie. Robi się to z tzw. szeregów potęgowych. Nie wchodząc w szczegóły, okazuje się, że np.

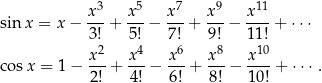
x3 x 5 x7 x 9 x11 sinx = x− ---+ ---− ---+ ---− ----+ ⋅⋅⋅ 3! 5! 7! 9! 11! x2- x4- x6- x8- x10- cos x = 1 − 2! + 4! − 6! + 8! − 10! + ⋅⋅⋅ .

Z prawej strony tych równości mamy nieskończone sumy (czyli tzw. szeregi) i należy to tak rozumieć, że im więcej wyrazów weźmiemy tym mamy lepsze przybliżenie sinusa/cosinusa. To co jest ważne, to że z prawej strony mamy tylko operacje dodawania, mnożenia, odejmowania i dzielenia (nie tam w ogóle funkcji trygonometrycznych!), a z tym kalkulator radzi sobie doskonale. Przy okazji, podobnie liczy się logarytmy i pierwiastki.

Wersja PDF