Zadanie nr 3431844
Zbadaj przebieg zmienności funkcji 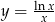 .
.
Rozwiązanie
Dziedziną podanej funkcji jest zbiór 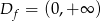 . Sprawdźmy, czy jest asymptota pionowa w
. Sprawdźmy, czy jest asymptota pionowa w 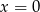 .
.
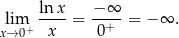
Zatem 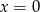 jest asympototą pionową.
jest asympototą pionową.
Sprawdźmy czy jest asymptota pozioma.
![lnx-[H] 1x- x→lim+ ∞ x = x→lim+ ∞ 1 = 0.](https://img.zadania.info/zad/3431844/HzadR4x.gif)
Zatem prosta 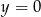 jest asymptotą poziomą w
jest asymptotą poziomą w 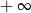 . Granicę policzyliśmy korzystając z reguły de l’Hospitala.
. Granicę policzyliśmy korzystając z reguły de l’Hospitala.
Zbadajmy teraz monotoniczność funkcji
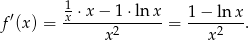
Widać zatem, że funkcja jest rosnąca na przedziale 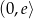 (pochodna jest dodatnia), oraz malejąca na przedziale
(pochodna jest dodatnia), oraz malejąca na przedziale 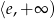 (pochodna jest ujemna). W punkcie
(pochodna jest ujemna). W punkcie  jest więc maksimum lokalne.
jest więc maksimum lokalne.
Zbadajmy teraz wypukłość funkcji.
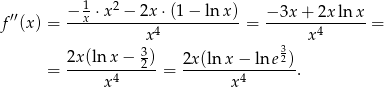
Widzimy zatem, że funkcja jest wklęsła na przedziale 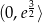 (druga pochodna ujemna) i wypukła na przedziale
(druga pochodna ujemna) i wypukła na przedziale 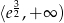 (druga pochodna dodatnia). W punkcie
(druga pochodna dodatnia). W punkcie 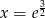 jest punkt przegięcia.
jest punkt przegięcia.
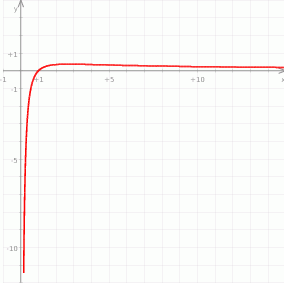
Możemy teraz naszkicować wykres funkcji.