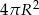Zadanie nr 3587985
Oblicz pole powierzchni sfery o promieniu 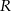 .
.
Rozwiązanie
Sposób I
Korzystamy ze wzoru
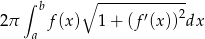
na pole powierzchni otrzymanej przez obrót wokół osi 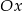 wykresu funkcji
wykresu funkcji 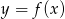 , gdzie
, gdzie ![x ∈ [a,b]](https://img.zadania.info/zad/3587985/HzadR3x.gif) .
.
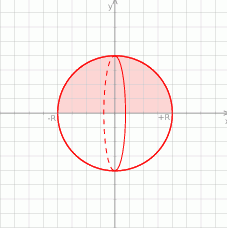
Sfera o promieniu 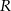 powstaje z obrotu wokół osi
powstaje z obrotu wokół osi 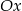 krzywej
krzywej

Mamy
![(∘ --------)′ −x f ′(x ) = R 2 − x2 = √--------, ∘ --------R2-− x2 ∘ ------------ 2 1+ [f ′(x )]2 = 1+ ---x----= √---r-----. R 2 − x 2 R 2 − x2](https://img.zadania.info/zad/3587985/HzadR8x.gif)
Zatem
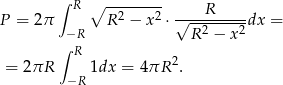
Sposób II
Tym razem policzmy pole powierzchni górnej półsfery, a na koniec wynik pomnożymy przez 2. O górnej półsferze możemy myśleć jak o wykresie funkcji 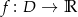 danej wzorem
danej wzorem 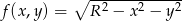 , gdzie
, gdzie 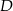 oznacza dysk
oznacza dysk 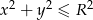 . Skorzystamy ze wzoru pole wykresu funkcji dwóch zmiennych
. Skorzystamy ze wzoru pole wykresu funkcji dwóch zmiennych
![∫ ∫ ∘ ----[---]-2--[---]-2 ∂f- ∂f- D 1 + ∂x + ∂y dxdy](https://img.zadania.info/zad/3587985/HzadR14x.gif)
W naszej sytuacji mamy
![[ ] 2 [ ]2 2 ∂f- = --∘---−-2x------- = ------x------ ∂x 2 R 2 − x 2 − y 2 R 2 − x2 − y2 [ ] [ ] 2 ∂f 2 − 2y y2 --- = -∘---2----2----2- = --2----2---2-. ∂y 2 R − x − y R − x − y](https://img.zadania.info/zad/3587985/HzadR15x.gif)
Zatem
![∘ ----[---]----[---]-- ∘ ------------- ∫ ∫ ∂f 2 ∂f 2 ∫∫ R2 1 + --- + --- dxdy = -2----2----2dxdy = D ∂x ∂y ∫∫D R − x − y -------R------- = ∘ -2----2----2dxdy D R − x − y](https://img.zadania.info/zad/3587985/HzadR16x.gif)
Aby obliczyć ostatnią całkę zmieniamy współrzędne na biegunowe.
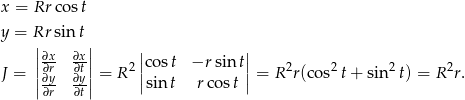
Zatem
![∫∫ R ∘--------------dxdy = D R2 − x2 − y2 ∫ 1 ∫ 2π R = ∘------------------------------⋅R 2rdtdr = 0 0 R 2 − R 2r2co s2 t− R 2r2sin2 t ∫ 1 ∫ 2π 1 ∫ 1 r ( ∫ 2π ) = √-------⋅R 2rdtdr = R 2 √------- 1dt dr = 0 0 1− r2 0 1 − r2 0 2∫ 1 r 2[∘ ------]1 2 = 2πR √------2dr = 2πR 1 − r2 = 2πR . 0 1− r 0](https://img.zadania.info/zad/3587985/HzadR18x.gif)
Zatem pole całej sfery jest równe 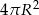 .
.
Sposób III
W obu poprzednich sposobach korzystaliśmy z gotowych wzorów – jeżeli chcemy tego uniknąć musimy odrobinę głębiej wejść w całkowanie 2-form. Chcemy policzyć całkę powierzchniową
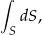
gdzie 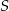 jest powierzchnią sfery o promieniu
jest powierzchnią sfery o promieniu 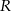 , a
, a 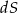 jest dwuwymiarową formą objętości na sferze. Aby obliczyć tę całkę używamy parametryzacji sferycznej
jest dwuwymiarową formą objętości na sferze. Aby obliczyć tę całkę używamy parametryzacji sferycznej
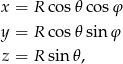
gdzie ![π π φ ∈ [0,2π ], 𝜃 ∈ [− 2, 2]](https://img.zadania.info/zad/3587985/HzadR25x.gif) .
.
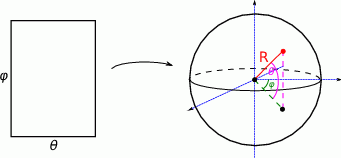
Jeżeli oznaczmy powyższą zmianę zmiennych przez 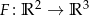 to
to
![∂F --- = [−R cos𝜃 sin φ ,R cos𝜃 cosφ ,0] ∂φ ∂F- ∂𝜃 = [−R sin 𝜃co sφ ,−R sin 𝜃sin φ,R cos 𝜃].](https://img.zadania.info/zad/3587985/HzadR28x.gif)
oraz
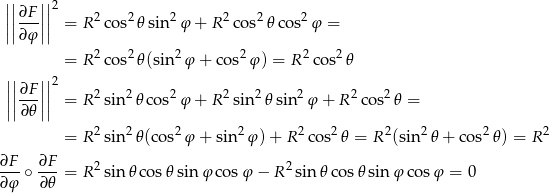
Jeżeli przez ![[ ] ∂F- J = ∂∂φF ∂𝜃](https://img.zadania.info/zad/3587985/HzadR30x.gif) oznaczymy macierz Jacobiego tej zmiany zmiennych to
oznaczymy macierz Jacobiego tej zmiany zmiennych to
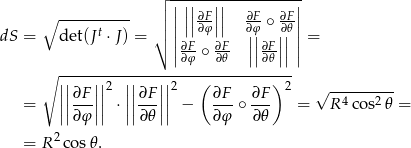
Zatem
![∫ ∫ 2π ∫ π2 ∫ 2π π dS = R 2co s𝜃d𝜃d φ = R 2 [sin 𝜃]2πd φ = S 0 − π2 0 − 2 ∫ 2π = 2R 2 1d φ = 4πR 2. 0](https://img.zadania.info/zad/3587985/HzadR32x.gif)
Odpowiedź: