Zadanie nr 3769349
Oblicz całkę 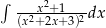 .
.
Rozwiązanie
W mianowniku mamy nierozkładalną funkcję kwadratową w drugiej potędze, więc szukamy rozkładu na dwa ułamki proste drugiego rodzaju.
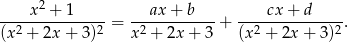
Mnożąc obie strony przez 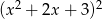 otrzymujemy
otrzymujemy
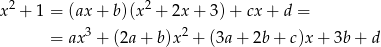
Porównując współczynniki przy kolejnych potęgach  otrzymujemy układ
otrzymujemy układ
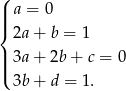
Z układu tego otrzymujemy 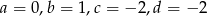 oraz
oraz
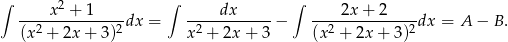
Aby obliczyć pierwszą powyższych całek skorzystamy ze wzoru
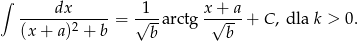
Liczymy
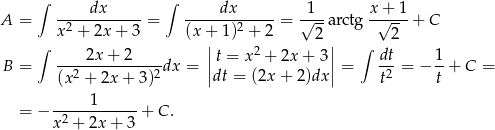
Mamy zatem
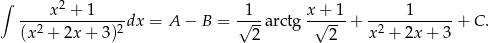
Odpowiedź: