Zadanie nr 3892325
Oblicz całkę 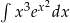 .
.
Rozwiązanie
Sposób I
Całkujemy przez części. Ponieważ 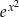 nie jest pochodną żadnej znanej nam funkcji, natomiast
nie jest pochodną żadnej znanej nam funkcji, natomiast 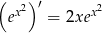 , więc przyjmiemy
, więc przyjmiemy 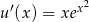 ,
, 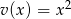 .
.
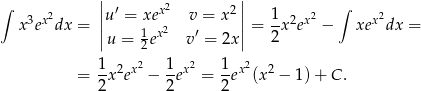
Sposób II
Podstawiamy w całce 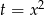 , a potem liczymy przez części.
, a potem liczymy przez części.
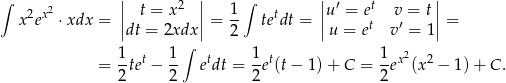
Odpowiedź: