Zadanie nr 3930304
Oblicz długość krzywej 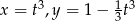 ,gdzie
,gdzie ![[ √ --] t ∈ 0, 3](https://img.zadania.info/zad/3930304/HzadT1x.gif) .
.
Rozwiązanie
Korzystamy ze wzoru
![∫ b∘ ----------------- [x′(t)]2 + [y′(t)]2dt a](https://img.zadania.info/zad/3930304/HzadR0x.gif)
na długość krzywej o parametryzacji 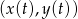 , gdzie
, gdzie ![t ∈ [a,b]](https://img.zadania.info/zad/3930304/HzadR2x.gif) .
.
W naszej sytuacji mamy
![x′(t) = 3t2 ′ 2 y (t) = −t √ - √- ∫ b ∘ ----------------- ∫ 3∘ -------- √ ---∫ 3 [x′(t)]2 + [y′(t)]2dt = 9t4 + t4dt = 10 t2dt = a √- 0 0 √ ---[1 ] 3 √ --- 1 √ -- √ --- = 10 --t3 = 10 ⋅--⋅3 3 = 30. 3 0 3](https://img.zadania.info/zad/3930304/HzadR3x.gif)
Odpowiedź: 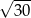
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz długość krzywej 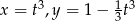 ,gdzie
,gdzie ![[ √ --] t ∈ 0, 3](https://img.zadania.info/zad/3930304/HzadT1x.gif) .
.
Korzystamy ze wzoru
![∫ b∘ ----------------- [x′(t)]2 + [y′(t)]2dt a](https://img.zadania.info/zad/3930304/HzadR0x.gif)
na długość krzywej o parametryzacji 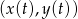 , gdzie
, gdzie ![t ∈ [a,b]](https://img.zadania.info/zad/3930304/HzadR2x.gif) .
.
W naszej sytuacji mamy
![x′(t) = 3t2 ′ 2 y (t) = −t √ - √- ∫ b ∘ ----------------- ∫ 3∘ -------- √ ---∫ 3 [x′(t)]2 + [y′(t)]2dt = 9t4 + t4dt = 10 t2dt = a √- 0 0 √ ---[1 ] 3 √ --- 1 √ -- √ --- = 10 --t3 = 10 ⋅--⋅3 3 = 30. 3 0 3](https://img.zadania.info/zad/3930304/HzadR3x.gif)
Odpowiedź: