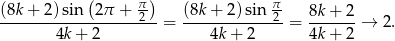Zadanie nr 4083908
Uzasadnij, że ciąg 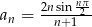 jest rozbieżny.
jest rozbieżny.
Rozwiązanie
Musimy pokazać dwa podciągi zbieżne do różnych granic.
Jeżeli 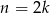 to mamy podciąg
to mamy podciąg
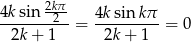
Jeżeli 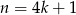 to mamy podciąg
to mamy podciąg
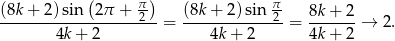
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Uzasadnij, że ciąg 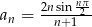 jest rozbieżny.
jest rozbieżny.
Musimy pokazać dwa podciągi zbieżne do różnych granic.
Jeżeli 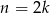 to mamy podciąg
to mamy podciąg
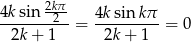
Jeżeli 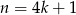 to mamy podciąg
to mamy podciąg