Zadanie nr 4188725
Oblicz granicę 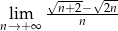 .
.
Rozwiązanie
Sposób I
Dzielimy licznik i mianownik przez 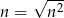 .
.
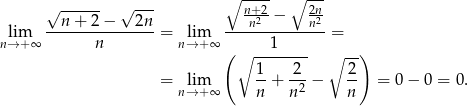
Sposób II
Skorzystamy ze wzoru 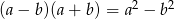 , żeby pozbyć się wyrażeń typu
, żeby pozbyć się wyrażeń typu  .
.
Liczymy
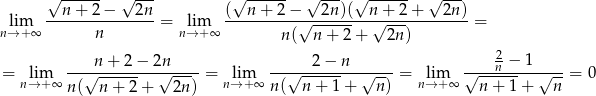
Odpowiedź: 0
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz granicę 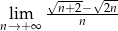 .
.
Sposób I
Dzielimy licznik i mianownik przez 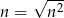 .
.
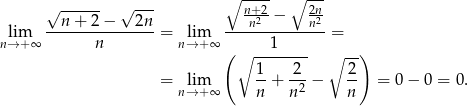
Sposób II
Skorzystamy ze wzoru 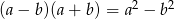 , żeby pozbyć się wyrażeń typu
, żeby pozbyć się wyrażeń typu  .
.
Liczymy
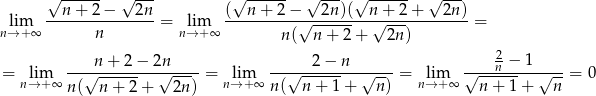
Odpowiedź: 0
