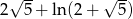Zadanie nr 4210507
Oblicz długość krzywej 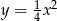 , gdzie
, gdzie 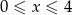 .
.
Rozwiązanie
Korzystamy ze wzoru
![∫ b ∘ ------------ 1+ [f′(x )]2dx a](https://img.zadania.info/zad/4210507/HzadR0x.gif)
na długość wykresu funkcji 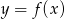 na przedziale
na przedziale ![[a,b]](https://img.zadania.info/zad/4210507/HzadR2x.gif) .
.
Szukana długość jest więc równa
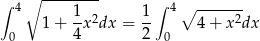
Korzystamy teraz ze wzoru
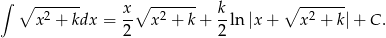
Mamy zatem
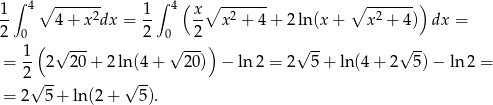
Odpowiedź: 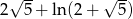
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz długość krzywej 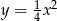 , gdzie
, gdzie 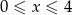 .
.
Korzystamy ze wzoru
![∫ b ∘ ------------ 1+ [f′(x )]2dx a](https://img.zadania.info/zad/4210507/HzadR0x.gif)
na długość wykresu funkcji 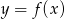 na przedziale
na przedziale ![[a,b]](https://img.zadania.info/zad/4210507/HzadR2x.gif) .
.
Szukana długość jest więc równa
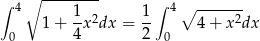
Korzystamy teraz ze wzoru
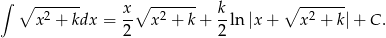
Mamy zatem
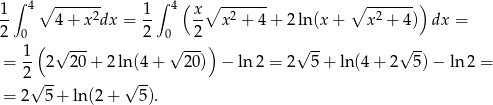
Odpowiedź: