Zadanie nr 4510452
Wyprowadź zależność rekurencyjną wiążącą 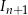 i
i 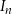 , jeżeli
, jeżeli
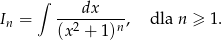
Rozwiązanie
Całkujemy przez części
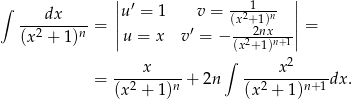
Ostatnią całkę przekształcamy
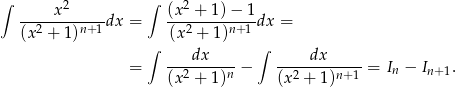
Podstawiając to wyrażenie do poprzedniej równości otrzymujemy
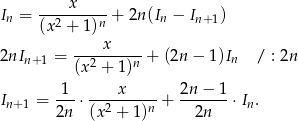
Odpowiedź: 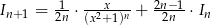
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wyprowadź zależność rekurencyjną wiążącą 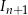 i
i 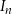 , jeżeli
, jeżeli
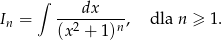
Całkujemy przez części
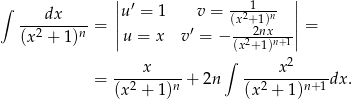
Ostatnią całkę przekształcamy
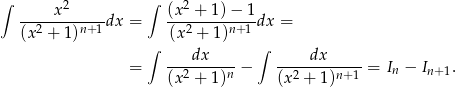
Podstawiając to wyrażenie do poprzedniej równości otrzymujemy
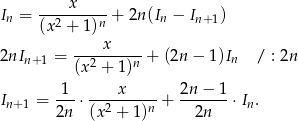
Odpowiedź: