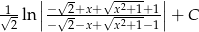Zadanie nr 4918162
Oblicz całkę 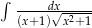 .
.
Rozwiązanie
Podstawiamy 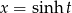 . Mamy wtedy
. Mamy wtedy 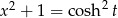 oraz
oraz
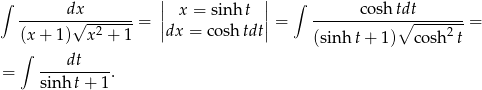
Aby obliczyć tę ostatnią całkę stosujemy podstawienie 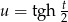 . Mamy wtedy
. Mamy wtedy 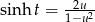 , oraz
, oraz
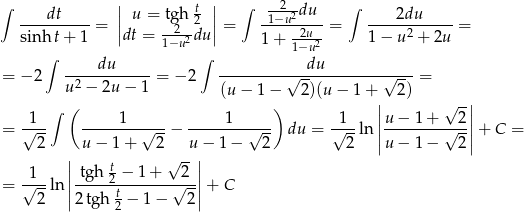
Teraz skorzystamy z równości 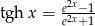 . Mamy więc
. Mamy więc
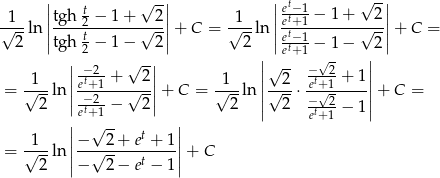
Pozostało teraz podstawić 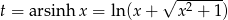 .
.
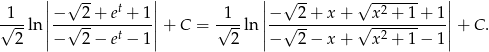
Odpowiedź: 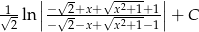
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 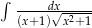 .
.
Podstawiamy 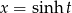 . Mamy wtedy
. Mamy wtedy 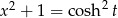 oraz
oraz
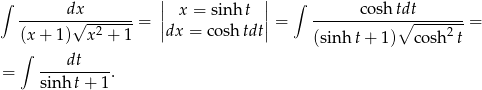
Aby obliczyć tę ostatnią całkę stosujemy podstawienie 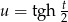 . Mamy wtedy
. Mamy wtedy 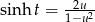 , oraz
, oraz
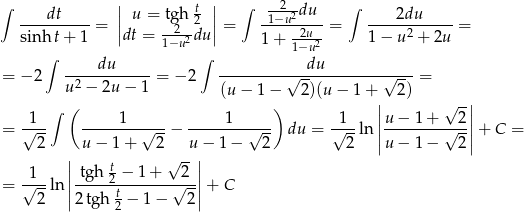
Teraz skorzystamy z równości 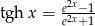 . Mamy więc
. Mamy więc
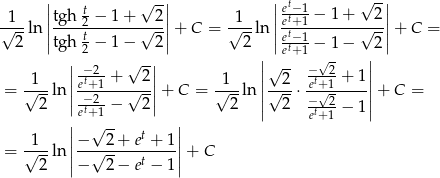
Pozostało teraz podstawić 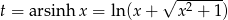 .
.
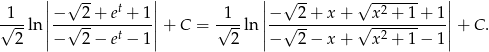
Odpowiedź: