Zadanie nr 5134982
Funkcja 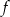 określona jest wzorem
określona jest wzorem 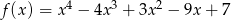 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 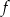 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 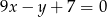 .
.
Rozwiązanie
Musimy sprawdzić w jakim punkcie styczna do wykresu 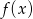 ma współczynnik kierunkowy równy 9. To pytanie to dokładnie pytanie, w jakim punkcie pochodna przyjmuje wartość 9. Liczymy
ma współczynnik kierunkowy równy 9. To pytanie to dokładnie pytanie, w jakim punkcie pochodna przyjmuje wartość 9. Liczymy
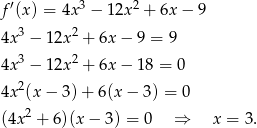
Odpowiadający punkt na wykresie to
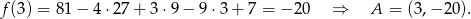
Szukana styczna ma więc równanie
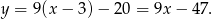
Na koniec obrazek dla ciekawskich.
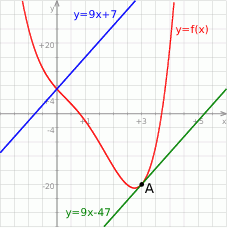
Odpowiedź: