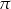Zadanie nr 5958061
Oblicz całkę 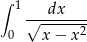 .
.
Rozwiązanie
Funkcja podcałkowa ma dwa punkty osobliwe w miejscach zerowych mianownika 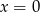 i
i 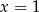 .
.
Liczymy całkę nieoznaczoną.
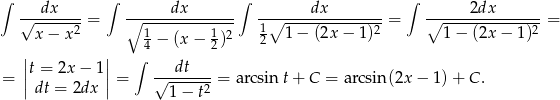
Stąd
![∫ 1 --dx----- 1 π- π- 0 √x-−--x2-= [arcsin(2x − 1)]0 = arcsin1 − a rcsin(− 1) = 2 + 2 = π.](https://img.zadania.info/zad/5958061/HzadR3x.gif)
Odpowiedź: 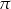
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 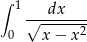 .
.
Funkcja podcałkowa ma dwa punkty osobliwe w miejscach zerowych mianownika 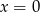 i
i 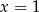 .
.
Liczymy całkę nieoznaczoną.
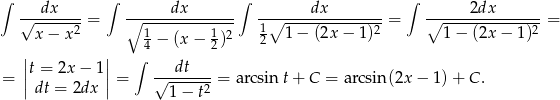
Stąd
![∫ 1 --dx----- 1 π- π- 0 √x-−--x2-= [arcsin(2x − 1)]0 = arcsin1 − a rcsin(− 1) = 2 + 2 = π.](https://img.zadania.info/zad/5958061/HzadR3x.gif)
Odpowiedź: