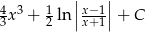Zadanie nr 6033220
Oblicz całkę 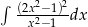 .
.
Rozwiązanie
Liczymy
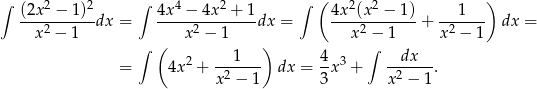
Ostatnią całkę liczymy zgadując rozkład na ułamki proste.
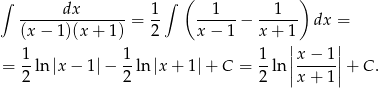
Mamy zatem
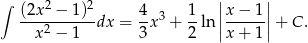
Odpowiedź: 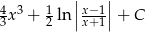
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 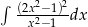 .
.
Liczymy
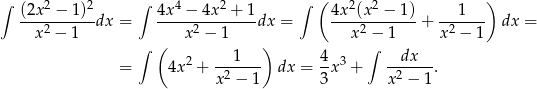
Ostatnią całkę liczymy zgadując rozkład na ułamki proste.
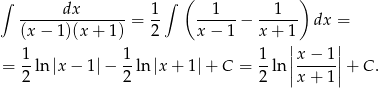
Mamy zatem
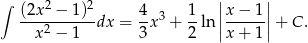
Odpowiedź: