Zadanie nr 6283558
Wyznacz przedziały monotoniczności i ekstrema lokalne funkcji 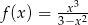 .
.
Rozwiązanie
Oczywiście liczymy pochodną.
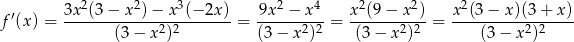
Widać stąd, że
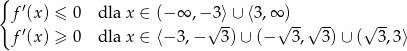
Zatem
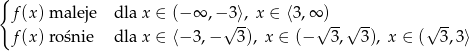
Z powyższej analizy widzimy, że 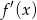 zmienia znak w punktach
zmienia znak w punktach 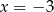 i
i 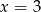 . W pierwszym z nich jest minimum a w
. W pierwszym z nich jest minimum a w 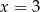 maksimum lokalne. Obliczamy jeszcze wartości w tych punktach.
maksimum lokalne. Obliczamy jeszcze wartości w tych punktach.
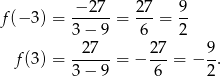
Dla ciekawskich wykres funkcji 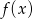 .
.
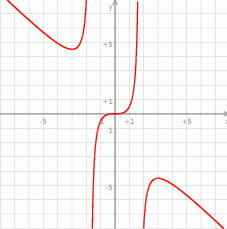
Odpowiedź: Minimum lokalne: 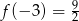 , maksimum lokalne:
, maksimum lokalne: 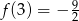 .
.

