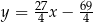Zadanie nr 6872240
Funkcja 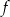 określona jest wzorem
określona jest wzorem 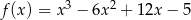 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 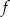 , które przechodzą przez punkt
, które przechodzą przez punkt 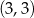 .
.
Rozwiązanie
Musimy sprawdzić w jakim punkcie styczna do wykresu  jest prostą przechodzącą przez punkt
jest prostą przechodzącą przez punkt 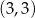 . Zacznijmy od wyznaczenia ogólnej postaci stycznej do danej funkcji w punkcie
. Zacznijmy od wyznaczenia ogólnej postaci stycznej do danej funkcji w punkcie 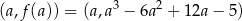 . Liczymy pochodną.
. Liczymy pochodną.
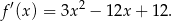
Styczna do paraboli w punkcie 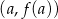 ma więc współczynnik kierunkowy równy
ma więc współczynnik kierunkowy równy 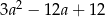 , czyli jest to prosta o równaniu
, czyli jest to prosta o równaniu
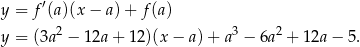
Sprawdzamy teraz kiedy styczna przechodzi przez dany punkt 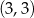 .
.
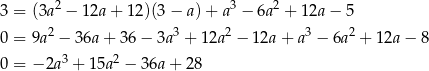
Szukamy teraz pierwiastków wymiernych tego wielomianu – łatwo sprawdzić, że jednym z nich jest 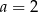 . Dzielimy więc ten wielomian przez
. Dzielimy więc ten wielomian przez 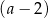 – my zrobimy to grupując wyrazy.
– my zrobimy to grupując wyrazy.
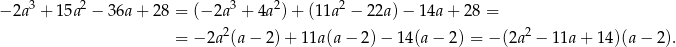
Rozkładamy jeszcze trójmian w pierwszym nawiasie.
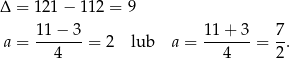
Zatem są dwie styczne spełniające warunki zadania: dla 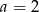 i
i 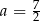 . Równanie pierwszej z nich to
. Równanie pierwszej z nich to
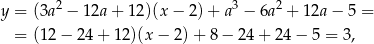
a równanie drugiej to
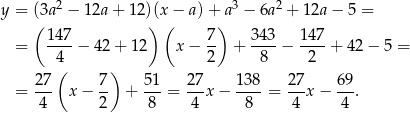
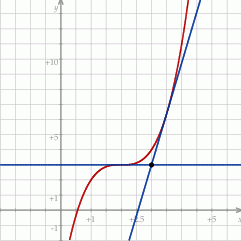
Odpowiedź: 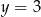 i
i