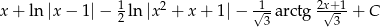Zadanie nr 6893015
Oblicz całkę 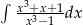 .
.
Rozwiązanie
Najpierw zmniejszamy stopień licznika.
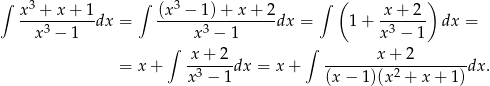
Funkcję pod ostatnią całką rozkładamy na ułamki proste
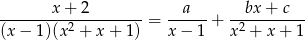
Mnożąc obie strony przez 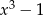 mamy
mamy
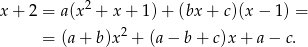
Porównując współczynniki przy kolejnych potęgach  mamy
mamy
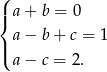
Dodając wszystkie trzy równania stronami mamy 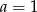 , skąd
, skąd 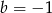 i
i 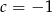 . Mamy zatem
. Mamy zatem
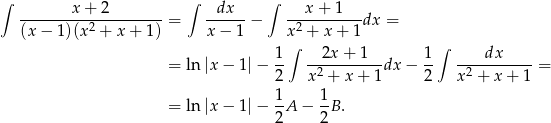
Pierwszą całkę liczymy podstawiając za mianownik, a drugą korzystając ze wzoru
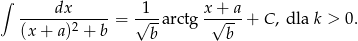
Liczymy
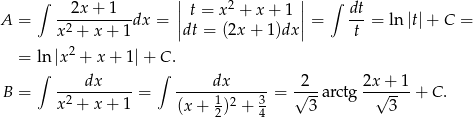
Mamy zatem
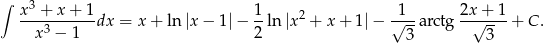
Odpowiedź: