Zadanie nr 7114600
Dodaj do ulubionych
Dodaj do rozwiązanych
Oblicz całkę 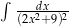 .
.
Rozwiązanie
Skorzystamy ze wzoru
Liczymy
Odpowiedź: 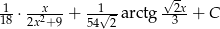
Twoje uwagi
Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!
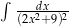 .
.  Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
