Zadanie nr 7321941
Wyznacz maksymalne przedziały monotoniczności funkcji 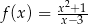 określonej dla
określonej dla 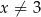 .
.
Rozwiązanie
Obliczamy pochodną funkcji 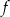 - skorzystamy ze wzoru:
- skorzystamy ze wzoru:
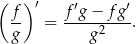
Mamy zatem
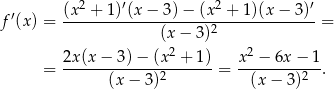
Mianownik tego wyrażenia jest zawsze dodatni. Rozkładamy jego licznik
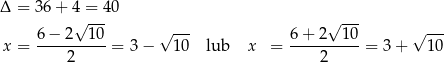
Zatem
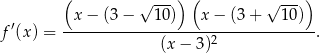
To oznacza, że pochodna jest dodatnia w przedziałach
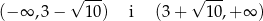
oraz ujemna w przedziałach
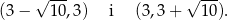
Funkcja 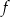 jest więc rosnąca w przedziałach
jest więc rosnąca w przedziałach
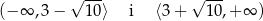
oraz malejąca w
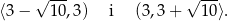
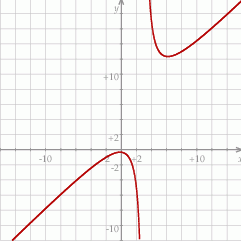
Na koniec dla ciekawskich wykres funkcji 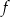 .
.
Odpowiedź: Ros. w 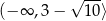 ,
, 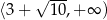 , mal. w
, mal. w 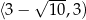 i
i 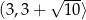 .
.

