Zadanie nr 7369236
Oblicz całkę 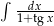 .
.
Rozwiązanie
Zauważmy, że jeżeli podstawimy 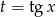 to
to
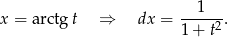
Zatem
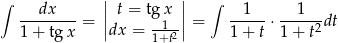
Otrzymaną całkę liczymy szukając rozkładu na ułamki proste.
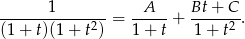
Mnożymy obie strony przez 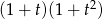 .
.
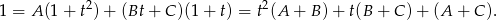
Mamy stąd układ równań
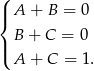
Dodając dwa pierwsze równania stronami i odejmując trzecie otrzymujemy 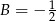 . Stąd
. Stąd 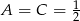 oraz
oraz
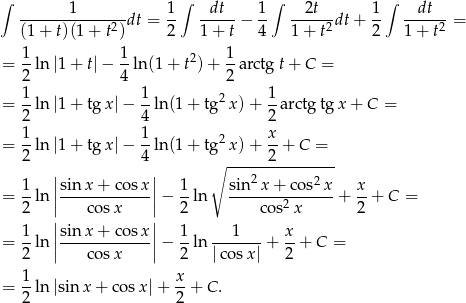
Odpowiedź: