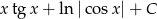Zadanie nr 7493985
Oblicz całkę 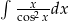 .
.
Rozwiązanie
Zauważmy, że 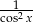 jest pochodną funkcji
jest pochodną funkcji 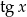 , więc naturalne jest całkowanie części.
, więc naturalne jest całkowanie części.
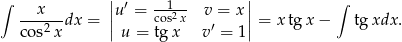
Całkę 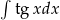 obliczymy przez podstawienie
obliczymy przez podstawienie 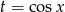 .
.
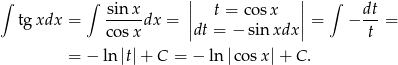
Zatem
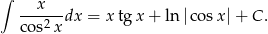
Odpowiedź: 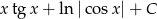
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 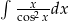 .
.
Zauważmy, że 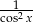 jest pochodną funkcji
jest pochodną funkcji 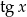 , więc naturalne jest całkowanie części.
, więc naturalne jest całkowanie części.
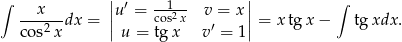
Całkę 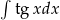 obliczymy przez podstawienie
obliczymy przez podstawienie 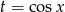 .
.
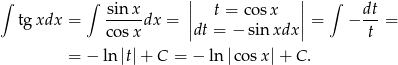
Zatem
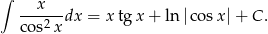
Odpowiedź: