Zadanie nr 7916871
Prosta o równaniu 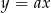 przecina parabolę o równaniu
przecina parabolę o równaniu 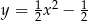 w dwóch punktach
w dwóch punktach 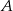 i
i 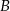 . Wykaż, że styczne do tej paraboli w punktach
. Wykaż, że styczne do tej paraboli w punktach 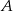 i
i 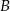 są prostopadłe.
są prostopadłe.
Rozwiązanie
Szkicujemy opisaną sytuację.
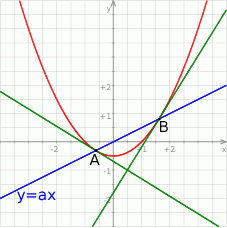
Musimy najpierw wyznaczyć pierwsze współrzędne punktów wspólnych danej prostej i paraboli – podstawiamy 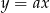 do równania paraboli.
do równania paraboli.
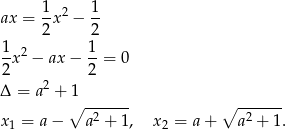
Liczymy pochodną
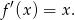
Współczynniki interesujących nas stycznych są więc równe
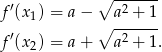
Teraz wystarczy zauważyć, że
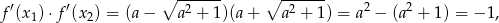
co dowodzi, że styczne rzeczywiście są prostopadłe.

