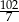Zadanie nr 7972729
Oblicz całkę 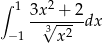 .
.
Rozwiązanie
Funkcja podcałkowa ma jeden punkt osobliwy 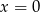 . Liczymy całkę nieoznaczoną
. Liczymy całkę nieoznaczoną
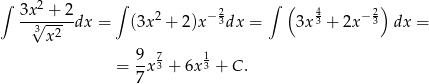
Zatem
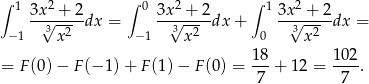
Odpowiedź: 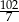
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 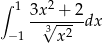 .
.
Funkcja podcałkowa ma jeden punkt osobliwy 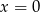 . Liczymy całkę nieoznaczoną
. Liczymy całkę nieoznaczoną
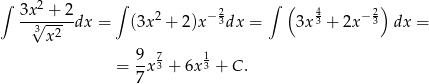
Zatem
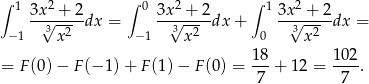
Odpowiedź: