Zadanie nr 7985978
Oblicz granicę 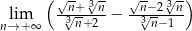 .
.
Rozwiązanie
Sposób I
Liczymy
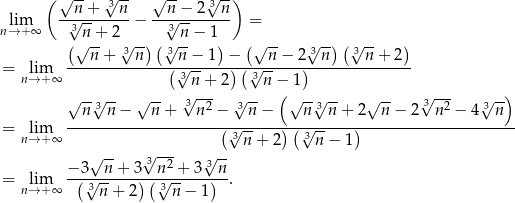
Dzielimy teraz licznik i mianownik przez 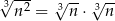 .
.
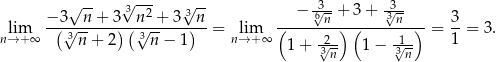
Sposób II
Jeżeli nie mamy ochoty przekształcać wyrażenia z pierwiastkami, to możemy podstawić 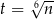 . Jeżeli
. Jeżeli 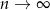 , to też
, to też 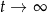 i mamy
i mamy
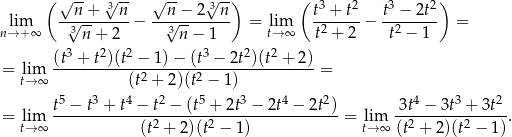
Dzielimy teraz licznik i mianownik przez 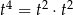 .
.
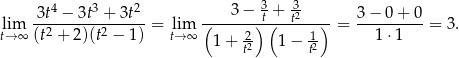
Odpowiedź: 3

