Zadanie nr 8535809
Oblicz całkę 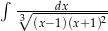 .
.
Rozwiązanie
Ponieważ
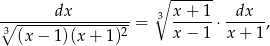
możemy podstawić 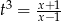 . Mamy wtedy
. Mamy wtedy
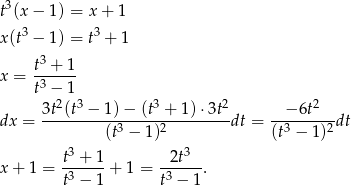
Stąd
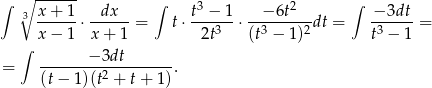
Rozkładamy teraz wyrażenie podcałkowe na ułamki proste.
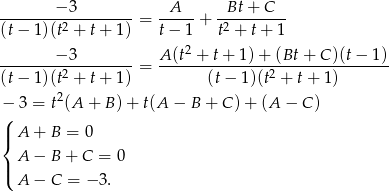
Podstawiając 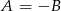 w drugim i trzecim równaniu otrzymujemy układ równań
w drugim i trzecim równaniu otrzymujemy układ równań
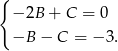
Dodajemy teraz równania stronami i otrzymujemy 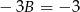 , czyli
, czyli 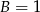 . Stąd
. Stąd 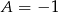 i
i 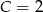 . Mamy więc
. Mamy więc
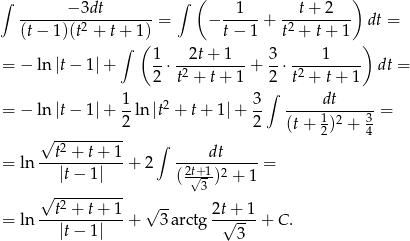
Odpowiedź: 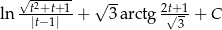 , gdzie
, gdzie