Zadanie nr 8676319
Oblicz granicę 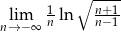 .
.
Rozwiązanie
Żeby nie mieć granicy w 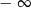 , zamieńmy
, zamieńmy  na
na 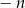 .
.
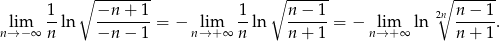
Zauważmy teraz, że
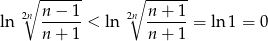
oraz
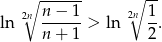
Ponadto 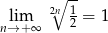 , więc na mocy twierdzenia o trzech ciągach szukana granica wynosi 0.
, więc na mocy twierdzenia o trzech ciągach szukana granica wynosi 0.
Odpowiedź: 0
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz granicę 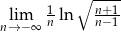 .
.
Żeby nie mieć granicy w 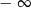 , zamieńmy
, zamieńmy  na
na 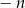 .
.
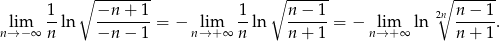
Zauważmy teraz, że
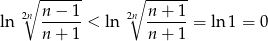
oraz
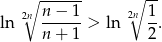
Ponadto 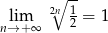 , więc na mocy twierdzenia o trzech ciągach szukana granica wynosi 0.
, więc na mocy twierdzenia o trzech ciągach szukana granica wynosi 0.
Odpowiedź: 0
