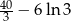/Studia/Analiza

Zadanie nr 8750226

Dodaj do ulubionych
Dodaj do rozwiązanych

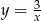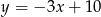Oblicz pole obszaru ograniczonego hiperbolą 3 y = x i prostą y = − 3x+ 10 .

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

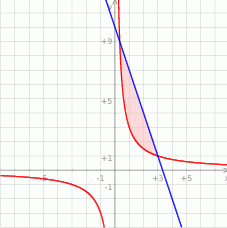
Widać, że wykresy danych funkcji przetną się w dwóch punktach, sprawdźmy w jakich.

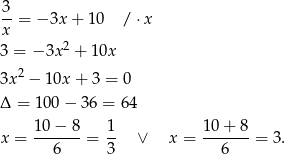
3-= − 3x + 1 0 / ⋅x x 3 = − 3x2 + 10x 3x 2 − 10x + 3 = 0 Δ = 10 0− 3 6 = 64 10-−-8- 1- 10-+-8- x = 6 = 3 ∨ x = 6 = 3.

Zatem interesujące nas pole jest równe

∫ ( ) [ ]3 3 3- 3-2 1 − 3x + 10 − x dx = − 2x + 10x − 3lnx 1 = 3 ( ) 3 27- 3- 1- 10- 1- = − 2 + 30 − 3ln 3− − 2 ⋅ 9 + 3 − 3ln 3 = = −-81+--180+--1−--20-− 3 ln 3 − 3ln 3 = 40-− 6ln 3. 6 3

 
Odpowiedź: 403 − 6 ln 3

Wersja PDF