Zadanie nr 8985092
Oblicz całkę 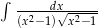 .
.
Rozwiązanie
Podstawiamy 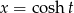 , gdzie
, gdzie 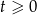 . Mamy wtedy
. Mamy wtedy 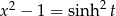 oraz
oraz
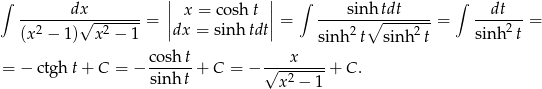
Uważny czytelnik powinien zauważyć, że licząc całkę przy pomocy podstawienia 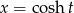 ograniczyliśmy dziedzinę funkcji podcałkowej do przedziału
ograniczyliśmy dziedzinę funkcji podcałkowej do przedziału 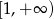 . Ponieważ jednak funkcja ta jest parzysta, a otrzymany wynik jest nieparzysty, to wynik ten jest poprawny bez tego ograniczenia.
. Ponieważ jednak funkcja ta jest parzysta, a otrzymany wynik jest nieparzysty, to wynik ten jest poprawny bez tego ograniczenia.
Odpowiedź: