Zadanie nr 9170596
Oblicz odległość między stycznymi do wykresu funkcji 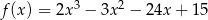 , które są równoległe do prostej
, które są równoległe do prostej 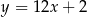 .
.
Rozwiązanie
Liczymy pochodną danej funkcji
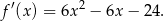
Szukamy teraz punktów, w których styczna ma współczynnik kierunkowy 12.
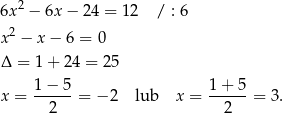
Zauważmy jeszcze, że
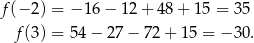
Interesujące nas styczne przechodzą więc przez punkty 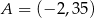 i
i 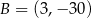 . Napiszmy jeszcze równanie jednej z tych stycznych, np. stycznej przechodzącej przez punkt
. Napiszmy jeszcze równanie jednej z tych stycznych, np. stycznej przechodzącej przez punkt 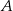 .
.
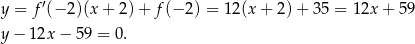
Pozostało obliczyć odległość punktu 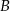 od tej prostej
od tej prostej
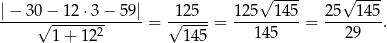
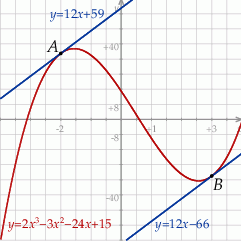
Na koniec obrazek dla ciekawskich.
Odpowiedź: