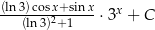Zadanie nr 9241444
Oblicz całkę 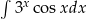 .
.
Rozwiązanie
Całkujemy przez części.
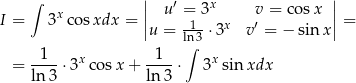
Zatem
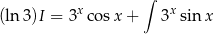
i możemy raz jeszcze całkować przez części.
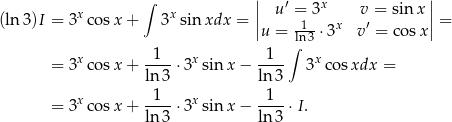
Zatem
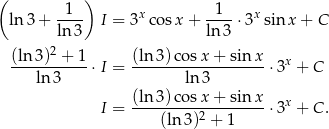
Odpowiedź: 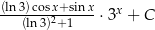
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 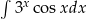 .
.
Całkujemy przez części.
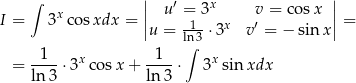
Zatem
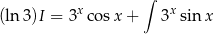
i możemy raz jeszcze całkować przez części.
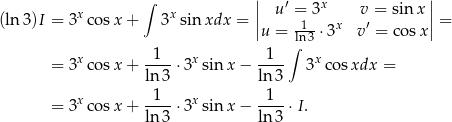
Zatem
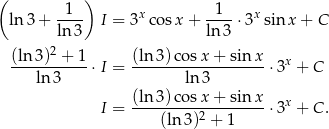
Odpowiedź: