Zadanie nr 9448353
Oblicz całkę 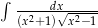 .
.
Rozwiązanie
Sposób I
Podstawiamy 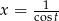 , gdzie
, gdzie ![t ∈ [0 ,π]](https://img.zadania.info/zad/9448353/HzadR1x.gif) . Zauważmy, że ponieważ funkcja pod znakiem całki jest parzysta, możemy policzyć całkę przy założeniu, że
. Zauważmy, że ponieważ funkcja pod znakiem całki jest parzysta, możemy policzyć całkę przy założeniu, że 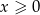 (czyli
(czyli ![t ∈ [0, π2-]](https://img.zadania.info/zad/9448353/HzadR3x.gif) ), a na koniec zrobimy z wyniku funkcję nieparzystą. Mamy zatem
), a na koniec zrobimy z wyniku funkcję nieparzystą. Mamy zatem
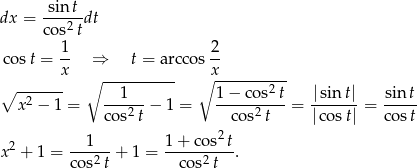
Zatem
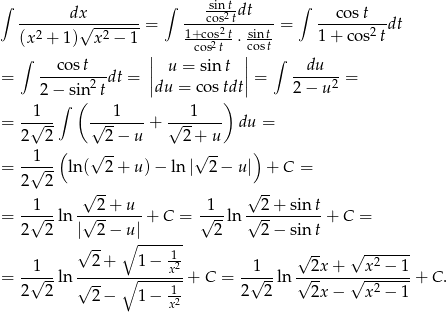
Można sprawdzić, że funkcja, którą otrzymaliśmy jest nieparzysta, więc wynik jest poprawny bez założenia 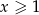 .
.
Sposób II
Podstawiamy 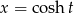 . Tak naprawdę to powinniśmy odrobinę uważać, bo
. Tak naprawdę to powinniśmy odrobinę uważać, bo  może być ujemny, a
może być ujemny, a 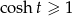 . Mamy jednak do czynienia z funkcją parzystą, więc wystarczy, że policzymy całkę dla
. Mamy jednak do czynienia z funkcją parzystą, więc wystarczy, że policzymy całkę dla 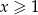 , a na koniec zrobimy z wyniku funkcję parzystą.
, a na koniec zrobimy z wyniku funkcję parzystą.
Druga uwaga, to 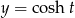 nie jest różnowartościowy, ale możemy założyć, że
nie jest różnowartościowy, ale możemy założyć, że 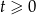 . Dzięki temu będziemy wiedzieć, że
. Dzięki temu będziemy wiedzieć, że 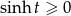 .
.
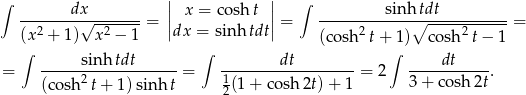
Teraz podstawiamy 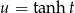 .
.
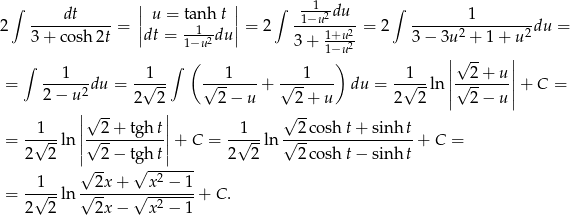
Po drodze opuściliśmy wartości bezwzględne, bo 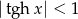 . Można sprawdzić, że funkcja, którą otrzymaliśmy jest nieparzysta, więc wynik jest poprawny bez założenia
. Można sprawdzić, że funkcja, którą otrzymaliśmy jest nieparzysta, więc wynik jest poprawny bez założenia 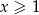 .
.
Odpowiedź: