Zadanie nr 9515621
Oblicz całkę 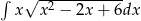 .
.
Rozwiązanie
Rozbijamy wyrażenie pod całką na dwie części tak, aby otrzymać pochodną trójmianu, który znajduje się pod pierwiastkiem.
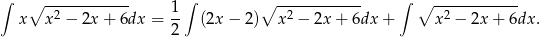
Pierwszą całkę liczymy podstawiając za trójmian pod pierwiastkiem
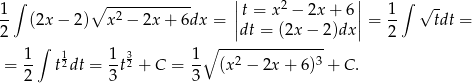
Drugą całkę policzymy korzystając ze wzoru
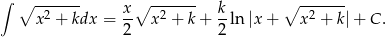
Liczymy
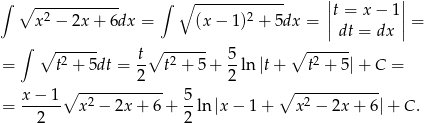
Mamy więc
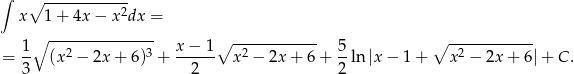
Odpowiedź: