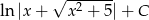/Studia/Analiza

Zadanie nr 9606429

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz całkę 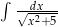∫ --dx-- √x2+5 .

Rozwiązanie

Sposób I

Korzystamy ze wzoru

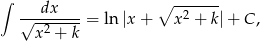
∫ dx ∘ ------- √--2-----= ln |x+ x2 + k|+ C, x + k

który łatwo jest wyprowadzić stosując podstawienie Eulera 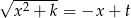√ ------- x2 + k = −x + t .

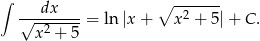
∫ ∘ ------- √--dx----= ln |x+ x2 + 5|+ C. x2 + 5

Sposób II

Jeżeli nie chcemy korzystać z podstawień Eulera to możemy podstawić 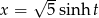√ -- x = 5sinh t oraz skorzystać ze wzoru

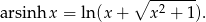
∘ ------- arsinh x = ln(x + x 2 + 1 ).

Liczymy

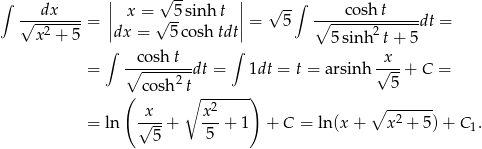
| √ -- | ∫ ---dx---- | x = 5sinh t | √ -∫ ----cosh-t----- √ -2-----= ||dx = √ 5-cosh tdt|| = 5 ∘ ------2-----dt = x + 5 ∫ ∫ 5 sin h t + 5 --cosh-t-- -x-- = ∘ -----2-dt = 1dt = t = a rsinh √ 5-+ C = ( co sh t∘ -------) x x2 ∘ ------- = ln √---+ ---+ 1 + C = ln(x + x2 + 5)+ C1. 5 5

 
Odpowiedź: √ -2----- ln |x+ x + 5|+ C

Wersja PDF