/Studia/Analiza

Zadanie nr 9842759

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz całkę niewłaściwą 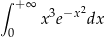∫ +∞ 2 x3e−x dx 0 .

Rozwiązanie

Najpierw obliczymy całkę nieoznaczoną. Całkujemy przez części.

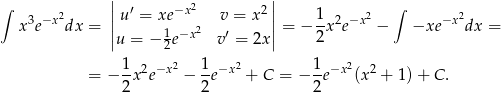
∫ || ′ −x 2 2 || ∫ x3e−x 2dx = ||u = xe v = x ||= − 1x2e−x 2 − −xe −x2dx = |u = − 1e−x2 v′ = 2x | 2 2 = − 1-x2e−x2 − 1-e−x 2 + C = − 1-e−x2(x2 + 1) + C. 2 2 2

Zatem funkcja podcałkowa ma funkcję pierwotną 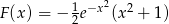F(x) = − 1 e−x 2(x2 + 1) 2 . Mamy 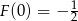1 F (0) = − 2 , a granicę 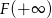F (+ ∞ ) obliczymy korzystając z reguły de L’Hospitala.

2 F(+ ∞ ) = lim − 1-⋅ x-+-1-= lim − 1-⋅--2x--= lim − 1-⋅-1- = 0. x→ +∞ 2 ex2 x→ +∞ 2 2xex 2 x→ +∞ 2 ex2

Stąd

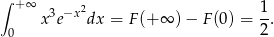
∫ + ∞ 3 −x2 1 x e dx = F(+ ∞ ) − F(0) = 2. 0

 
Odpowiedź: 1 2

Wersja PDF