/Studia/Analiza

Zadanie nr 9908072

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz pole obszaru zawartego pomiędzy parabolą 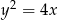2 y = 4x i prostą y = 2x− 4 .

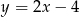Rozwiązanie

Aby wyznaczyć punkty przecięcia tych linii rozwiązujemy równanie kwadratowe

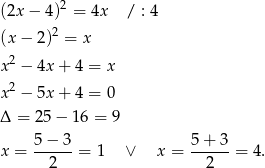
2 (2x − 4) = 4x / : 4 (x − 2)2 = x x2 − 4x + 4 = x 2 x − 5x + 4 = 0 Δ = 25− 16 = 9 5 − 3 5+ 3 x = ------= 1 ∨ x = ------= 4 . 2 2

Zatem dane krzywe przecinają się w punktach 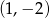(1 ,−2 ) i (4,4) .

PIC

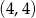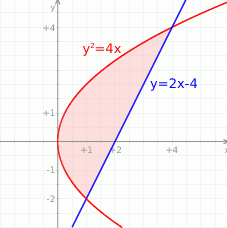
Zauważmy, że interesujący nas obszar możemy opisać nierównościami

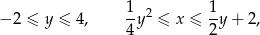
− 2 ≤ y ≤ 4, 1-y2 ≤ x ≤ 1y + 2, 4 2

zatem jego pole równa się

∫ 4 [ 2] [ 2 3]4 y+ 2− y-- dy = y--+ 2y − y-- = − 2 2 4 4 12 − 2 ( ) ( ) = 4+ 8− 16- − 1 − 4 + 2- = 9. 3 3

 
Odpowiedź: 9

Wersja PDF