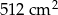Zadanie nr 4705199
Na okręgu o promieniu 8 cm opisano trapez. Kąty, które tworzą ramiona z dłuższą podstawą mają miarę 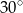 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
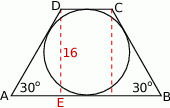
Z podanych informacji wynika, że trapez jest równoramienny oraz jego wysokość ma długość 16 cm. Ponadto 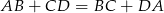 (tę własność ma każdy czworokąt opisany na okręgu). Mamy
(tę własność ma każdy czworokąt opisany na okręgu). Mamy
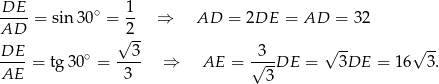
Sposób I
Korzystamy teraz z równości 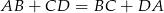 .
.
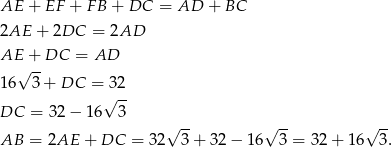
Liczymy teraz pole
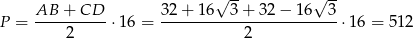
Sposób II
Pole dowolnego wielokąta opisanego na okręgu można obliczyć ze wzoru 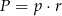 , gdzie
, gdzie 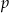 – połowa obwodu, a
– połowa obwodu, a  – promień okręgu wpisanego w wielokąt. W naszej sytuacji
– promień okręgu wpisanego w wielokąt. W naszej sytuacji 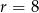 , a połowa obwodu to dokładnie
, a połowa obwodu to dokładnie 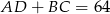 (dzięki równości
(dzięki równości 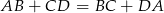 ). Zatem
). Zatem
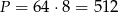
Odpowiedź: